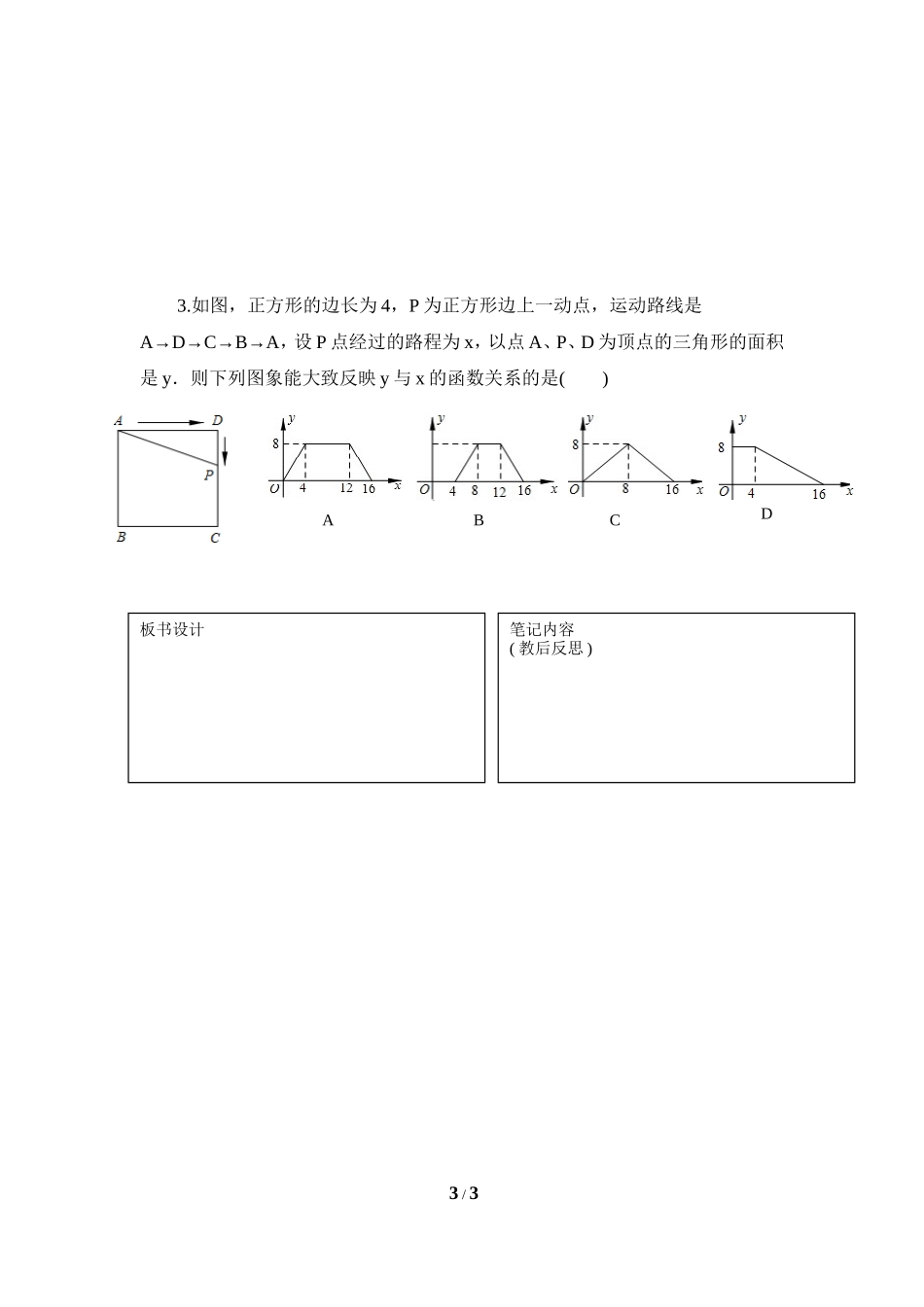
3.1对函数的再认识(2)导学案●学习目标:知识技能目标:会确定自变量取值范围;过程方法目标:进一步体验变量之间的数量关系;情感态度目标:通过函数的学习,体会事物是相互联系的,有规律的变化的.●重点难点:重点:会求简单函数的自变量取值范围及函数值.难点:会根据实际问题求出函数关系式.●学习过程【自主学习】1.导入:通过上节课的函数例子可以发现,这些函数都是用数学式子表示的.你知道函数还可以用什么方法表示吗?2.自学课本P65做一做中的内容并思考解答其中的问题。(会发现做一做中的(1)分析的依据是一张表格,做一做中的(2)分析的依据是一种图象)【合作交流】探究1:用来表示函数关系的方法都有哪些?探究2:这些方法都有哪些优点与不足?【典例学习】[例3]求下列函数的自变量x的取值范围:(1)(2)(3)(4)[例4]用总长为60m的篱笆围成矩形场地,求矩形的面积S(m2)与它的一边长x(m)之间的关系式,并求出x的取值范围.1/3ABCD升华理解:如何确定自变量的取值范围?【跟踪训练】A类:完成课本P67随堂练习第1,2题.B类:完成课本P68习题3.2第3题.【课堂小结】1.本节课你掌握了哪些知识?2.还有哪些困惑?3.掌握了哪些数学思想?【达标检测】A类:完成课本P68习题3.2第1,2题.B类:1.一个游泳池内有水90立方米,设排尽全水池的时间为t(分),每分钟的排水量为x(立方米),规定排水时间至少9分钟,至多15分钟,试写出排水时间t关于每分钟排水量x的函数解析式,并指出函数的自变量的取值范围.2.如图所示,在△ABC中,已知∠B,∠C的平分线相交于点D,设∠A和∠BDC的度数分别为x和y,求y与x之间的函数关系式,并求x的取值范围。2/33.如图,正方形的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是()3/3板书设计笔记内容(教后反思)ABCD