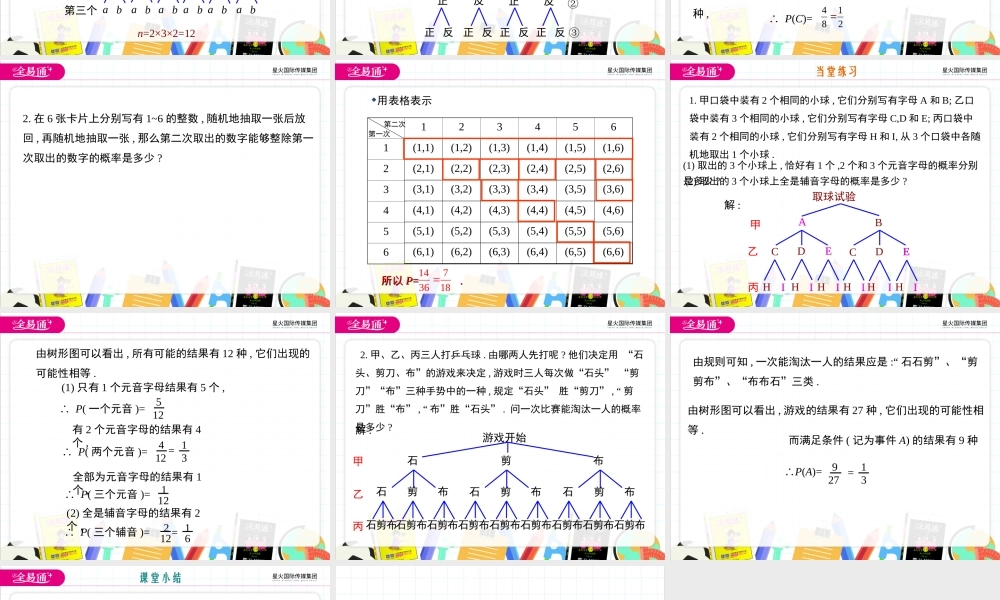
第25章随机事件的概率25.2随机事件的概率第3课时1.会用列表法、画树形图法计算概率;(重点)2.并通过比较概率大小做出合理决策.(难点)学习目标问题1什么时候用“列表法”方便?什么时候用“树状图法”方便?问题2如何用“列表法”、“树状图法”?回顾与思考当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.一个因素所包含的可能情况另一个因素所包含的可能情况两个因素所组合的所有可能情况,即n在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.列表法中表格构造特点:当一次试验中涉及3个因素或更多的因素时,用列表法就不方便了.为了不重不漏地列出所有可能的结果,通常采用“树状图”.一个试验第一个因素第二个第三个AB123123ababababababn=2×3×2=121.同时抛掷三枚硬币,求下列事件的概率:(1)三枚硬币全部正面朝上;(2)两枚硬币正面朝上而一枚硬币反面朝上;(3)至少有两枚硬币正面朝上.正反正反正反正反正反正反正反抛掷硬币试验第①枚②③解:用树状图或列表法求概率由树状图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.∴P(A)=(1)满足三枚硬币全部正面朝上(记为事件A)的结果只有1种,∴P(B)=(2)满足两枚硬币正面朝上而一枚硬币反面朝上(记为事件B)的结果有3种,(3)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种,∴P(C)=818321842.在6张卡片上分别写有1~6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?123456123456第一次第二次用表格表示(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)所以所以PP=.=.1473618(1)取出的3个小球上,恰好有1个,2个和3个元音字母的概率分别是多少?1.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I,从3个口袋中各随机地取出1个小球.(2)取出的3个小球上全是辅音字母的概率是多少?取球试验甲乙丙ABCDECDEHIHIHIHIHIHI解:AEEIIIIII当堂练习由树形图可以看出,所有可能的结果有12种,它们出现的可能性相等.∴P(一个元音)=(1)只有1个元音字母结果有5个,512∴P(两个元音)=有2个元音字母的结果有4个,41213=∴P(三个元...