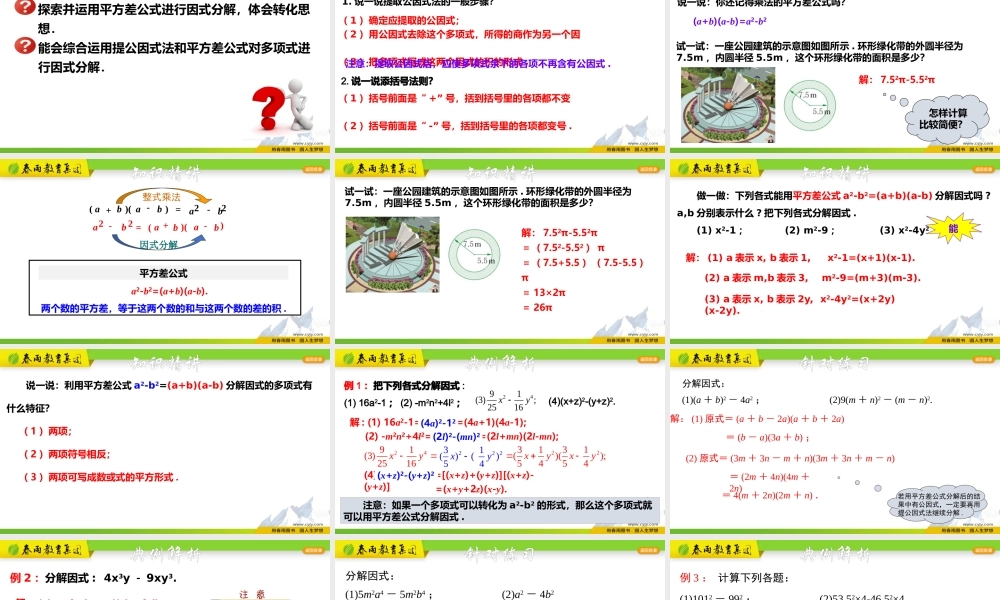
学习目标探索并运用平方差公式进行因式分解,体会转化思想.能会综合运用提公因式法和平方差公式对多项式进行因式分解.1.说一说提取公因式法的一般步骤?(1)确定应提取的公因式;(2)用公因式去除这个多项式,所得的商作为另一个因(3)把多项式写成这两个因式的积的形式.注意:提取公因式后,应使多项式余下的各项不再含有公因式.2.说一说添括号法则?(1)括号前面是“+”号,括到括号里的各项都不变(2)括号前面是“-”号,括到括号里的各项都变号.复习回顾说一说:你还记得乘法的平方差公式吗?(a+b)(a-b)=a2-b2试一试:一座公园建筑的示意图如图所示.环形绿化带的外圆半径为7.5m,内圆半径5.5m,这个环形绿化带的面积是多少?解:7.52π-5.52π怎样计算比较简便?知识精讲))((baba-+=22ba-))((22bababa-+=-整式乘法因式分解由乘法的平方差公式(a+b)(a-b)=a2-b2,可得:a2-b2=(a+b)(a-b).两个数的平方差,等于这两个数的和与这两个数的差的积.平方差公式知识精讲解:7.52π-5.52π=(7.52-5.52)π=(7.5+5.5)(7.5-5.5)π=13×2π=26π知识精讲试一试:一座公园建筑的示意图如图所示.环形绿化带的外圆半径为7.5m,内圆半径5.5m,这个环形绿化带的面积是多少?做一做:下列各式能用平方差公式a2-b2=(a+b)(a-b)分解因式吗?a,b分别表示什么?把下列各式分解因式.(1)x2-1;(2)m2-9;(3)x2-4y2.解:(1)a表示x,b表示1,x2-1=(x+1)(x-1).(3)a表示x,b表示2y,x2-4y2=(x+2y)(x-2y).(2)a表示m,b表示3,m2-9=(m+3)(m-3).能知识精讲说一说:利用平方差公式a2-b2=(a+b)(a-b)分解因式的多项式有什么特征?(1)两项;(2)两项符号相反;(3)两项可写成数或式的平方形式.知识精讲解:(1)16a2-1=(4a)2-12=(4a+1)(4a-1);(4)(x+z)2-(y+z)2=[(x+z)+(y+z)][(x+z)-(y+z)]242222291313131(3)()()()();2516545454xyxyxyxy例1:把下列各式分解因式:(1)16a2-1;(2)-m2n2+4l2;2491(3);2516xy(4)(x+z)2-(y+z)2.(2)-m2n2+4l2=(2l)2-(mn)2=(2l+mn)(2l-mn);=(x+y+2z)(x-y).(4a)2-12(2l)2-(mn)222231()()54xy(x+z)2-(y+z)2注意:如果一个多项式可以转化为a2-b2的形式,那么这个多项式就可以用平方差公式分解因式.典例解析分解因式:(1)(a+b)2-4a2;(2)9(m+n)2-(m-n)2.=(2m+4n)(4m+2n)解:(1)原式=(a+b-2a)(a+b+2a)=(b-a)(3a+b);(2)原式=(3m+3n-m+n)(3m+3n+m-n)=4(m+2n)(2m+n).若用平方差公式分解后的结果中有公因式,一...