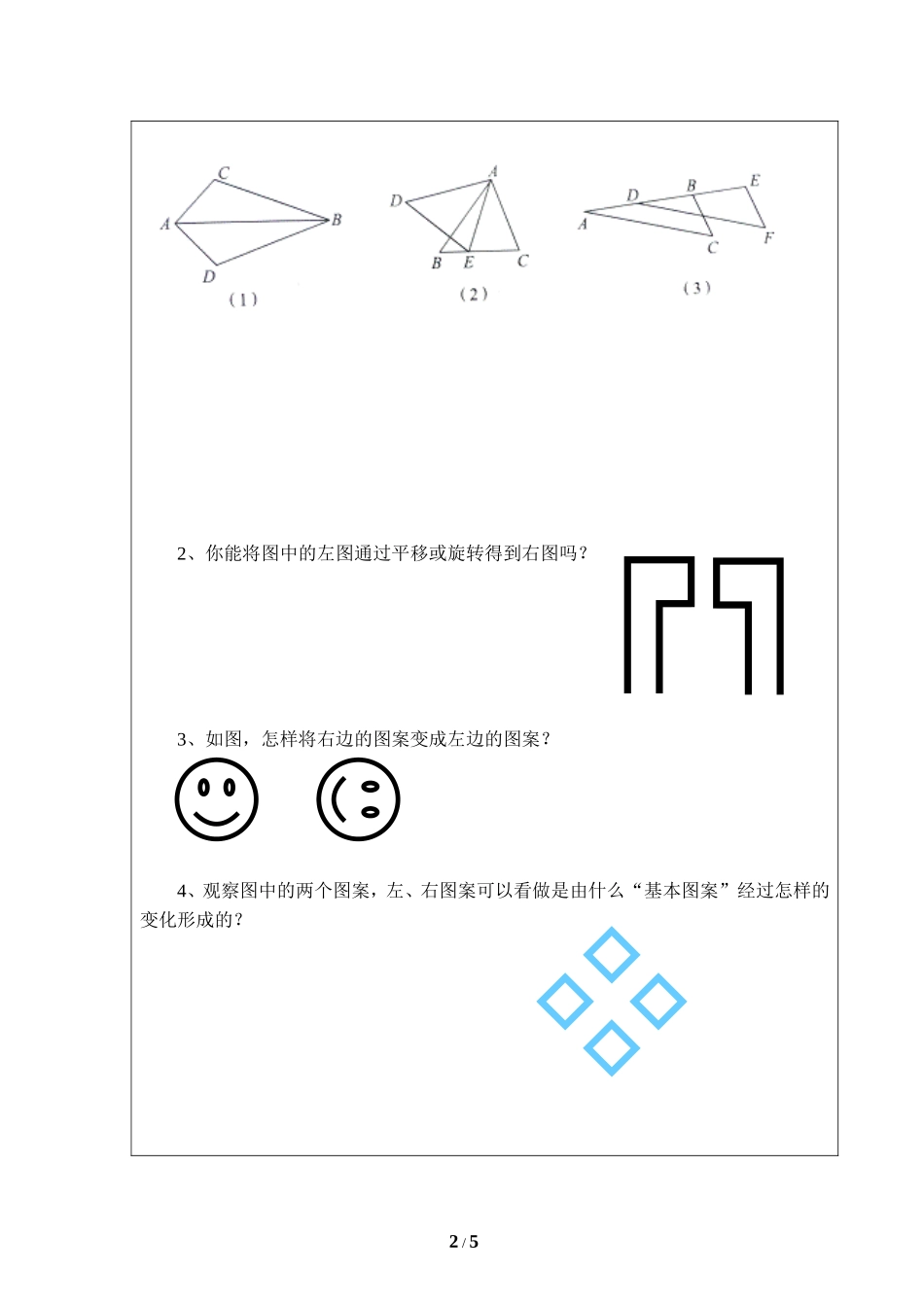
1/5课题:4.4图形变化的简单应用(1)课型:新授课一、学习目标:1.掌握平面图形的全等变换(轴对称,平移,旋转及其组合)的特征;2.经历探索图形之间的变换关系的过程,提高图形分析能力;3.能应用平面图形的全等变换解决问题.二、学习重点:重点:图形之间的变化的类型;难点:图案的欣赏与分析.三、自学指导:(一)、下图是由△和△组成的中心对称图形.A1B1C1ABC(1)请找出它的对称中心.(2)过点画一条直线,并画出△关于直线成轴对称的△.(3)将△进行平移变换可以得到△吗?旋转变换呢?四、典型例题例1、你能对甲图案进行适当的运动变化,使它与乙图案重合吗?写出你的操作过程.练习一1、观察下列各图,分别说明是怎样将△变成另一个与它全等的三角形的.2/52、你能将图中的左图通过平移或旋转得到右图吗?3、如图,怎样将右边的图案变成左边的图案?4、观察图中的两个图案,左、右图案可以看做是由什么“基本图案”经过怎样的变化形成的?3/5五、当堂检测1.(高青县)在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是()2.(杨浦区二模)下列每个图中都有一对全等三角形,其中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是()3.(海淀区二模)下列图形可以由一个图形经过平移变换得到的是()4.(本溪)下列各网格中的图形是用其图形中的一部分平移得到的是()5.经过平移或旋转不可能将甲图案变成乙图案的是()6.(淮安)下列基本图形中,经过平移、旋转或轴对称变换后,不能得到如图的是()4/57.如图是由三个等边三角形拼成的图形,它可以看成是由其中一个等边三角形经过怎样的变化得到的?8、如图,方格纸上的四边形是由四边形经过变换得到的,试说出它的变换过程?六、拓展提升1、(盐城)如图①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有()A、4种B、5种C、6种D、7种2、(宁德)如图,是用围棋子摆出的图案(用棋子的位置用用有序数对表示,如A点在(5,1)),如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是()A、黑(3,3),白(3,1)B、黑(3,1),白(3,3)C、黑(1,5),白(5,5)D、黑(3,2),白(3,3)BADCD'A'B'C'5/5