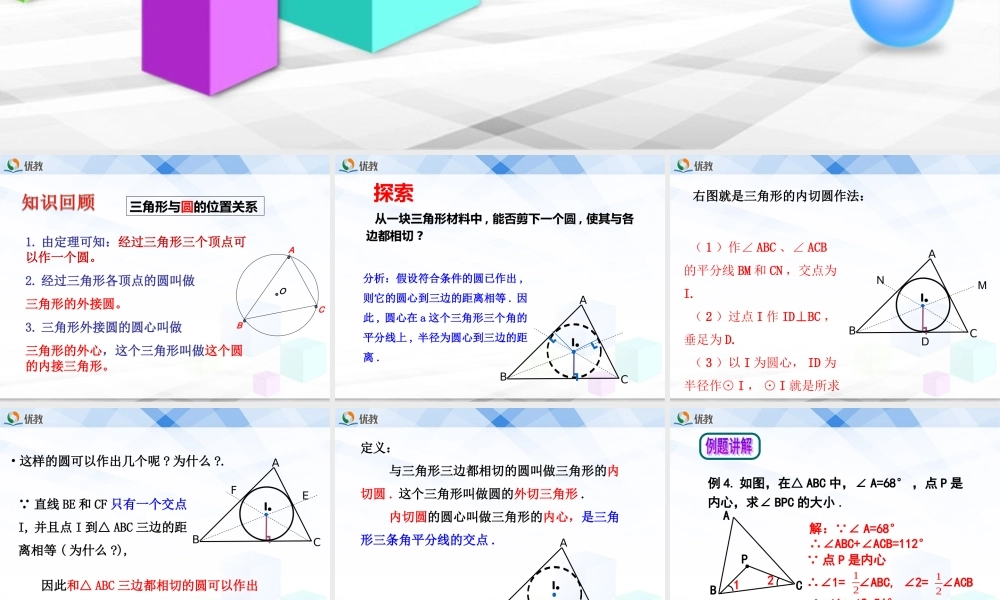
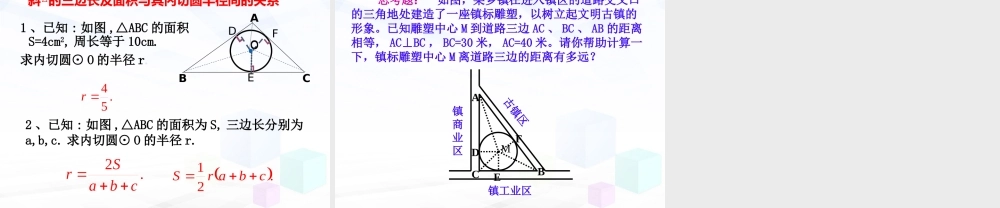
5.6直线和圆的位置关系(4)第五章圆O1.由定理可知:经过三角形三个顶点可以作一个圆。2.经过三角形各顶点的圆叫做三角形的外接圆。3.三角形外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。ABC三角形与圆的位置关系从一块三角形材料中,能否剪下一个圆,使其与各边都相切?分析:假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在a这个三角形三个角的平分线上,半径为圆心到三边的距离.ABC┓┗┗┓I●●●┓┗┗┓┗┗┓┗┗探索右图就是三角形的内切圆作法:(1)作∠ABC、∠ACB的平分线BM和CN,交点为I.(2)过点I作ID⊥BC,垂足为D.(3)以I为圆心,ID为半径作⊙I,⊙I就是所求ABCI●┓●DMN•这样的圆可以作出几个呢?为什么?. 直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.ABCI●┓●EF定义:与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.ABCI●●●例4.如图,在△ABC中,∠A=68°,点P是内心,求∠BPC的大小.CABP12解: ∠A=68°∴∠ABC+∠ACB=112° 点P是内心∴∠1+∠2=56°∴∠BPC=124°∴∠1=∠ABC,∠2=∠ACB1212如图,在△ABC中,点O是内心,(1)若∠ABC=50°,∠ACB=70°,求∠BOC的度数ABCO(2)若∠A=80°,则∠BOC=度。(3)若∠BOC=110°,则∠A=度。解(1) 点O是△ABC的内心,∴∠OBC=OBA=ABC=25°∠∠同理∠OCB=OCA=ACB=35°∠∠∴∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°121213040变式练习2121212121理由: 点O是△ABC的内心,∴∠OBC=ABC∠,∠OCB=ACB∠∴∠OBC+∠OCB=(∠ABC+ACB∠)=(180°-∠A)=90°-∠A∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-∠A)=90°+A∠212112答:∠BOC=90°+A∠(4)试探索:∠A与∠BOC之间存在怎样的数量关系?请说明理由。ABCO1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?345ABC2.分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?提示:先确定圆心和半径,尺规作图要保留作图痕迹.ABCABC●●●CAB┐判断题:1、三角形的内心到三角形各个顶点的距离相等()2、三角形的外心到三角形各边的距离相等()3、等边三角形的内心和外心重合;()4、三角形的内心一定在三角形的内部()5、菱形一定有...