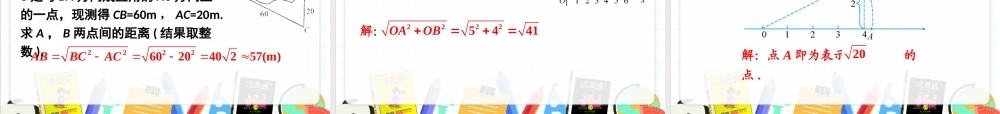17.1勾股定理第2课时1.能应用勾股定理计算直角三角形的边长.2.能应用勾股定理解决简单的实际问题.学习目标学习目标这节课我们就来学习用勾股定理解决实际问题.新课导入新课导入例1一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?已知条件有哪些?知识讲解知识讲解利用勾股定理解决实际问题利用勾股定理解决实际问题知识点1知识点1观察1.木板能横着或竖着从门框通过吗?2.这个门框能通过的最大长度是多少?不能3.怎样判定这块木板能否通过木框?求出斜边的长,与木板的宽比较.解:在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=12+22=5.AC=≈2.24.因为AC大于木板的宽2.2m,所以木板能从门框内通过.5例2如图,一架2.6米长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4米.(1)求梯子的底端B距墙角O多少米?(2)如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?CODBA在Rt△COD中,根据勾股定理,OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.解:在Rt△AOB中,根据勾股定理,OB2=AB2-OA2=2.62-2.42=1.OB=1.3151771771077OD..BDODOB...,1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A,B两点间的距离(结果取整数).解:2222602040257mABBCAC.即学即练即学即练ABC2.如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长为120cm.太阳能真空管AC有多长?【解析】在Rt△ABC中,由勾股定理,得AC===150(cm).答:太阳能真空管AC长150cm.思考在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等。学习了勾股定理后,你能证明这一结论吗?勾股定理的应用勾股定理的应用知识点2知识点2已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.求证:ABC≌△A′B′C′.证明:在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°根据勾股定理,得2222BCABAC,BCABAC.又AB=A′B′,AC=A′C′,∴BC=B′C′.∴ABC≌△A′B′C′(SSS).探究我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?1313开方就是,,如果一个三角形的斜边长为的话,问题就可迎刃而解了。1313发现是直角边分别为2,3的直角三角形的斜边长。132133O12313ABC你能用语言叙述一下作图过程吗?在数轴上找到点A,使OA=3;作直线l⊥OA,在l上取一点B,使AB=2;以原点O为圆心,以OB为半径作弧,...