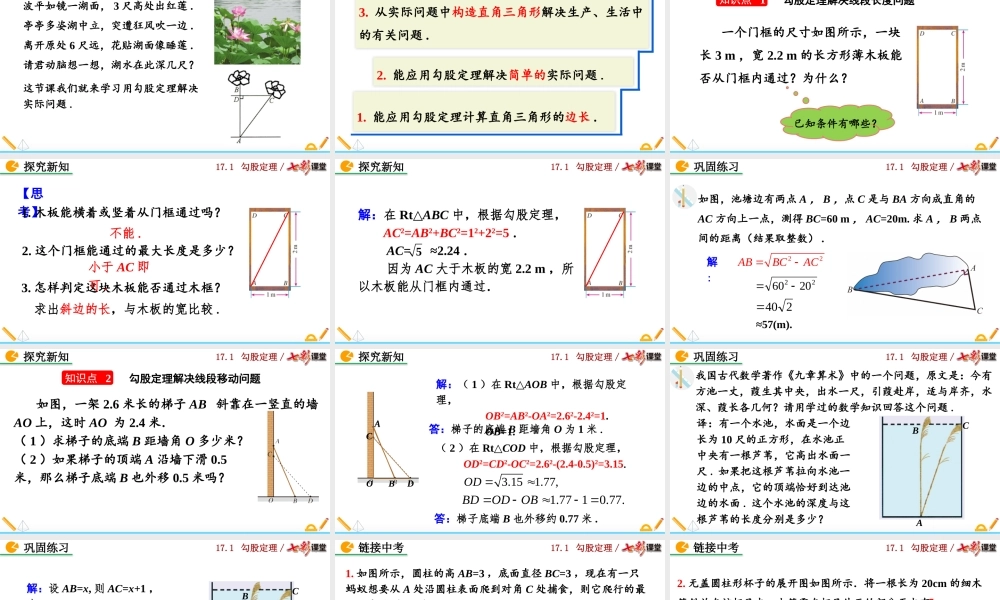
17.1勾股定理(第2课时)人教版数学八年级下册17.1勾股定理/这节课我们就来学习用勾股定理解决实际问题.导入新知波平如镜一湖面,3尺高处出红莲.亭亭多姿湖中立,突遭狂风吹一边.离开原处6尺远,花贴湖面像睡莲.请君动脑想一想,湖水在此深几尺?17.1勾股定理/2.能应用勾股定理解决简单的实际问题.1.能应用勾股定理计算直角三角形的边长.学习目标3.从实际问题中构造直角三角形解决生产、生活中的有关问题.17.1勾股定理/一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?已知条件有哪些?探究新知知识点1勾股定理解决线段长度问题17.1勾股定理/【思考】1.木板能横着或竖着从门框通过吗?2.这个门框能通过的最大长度是多少?不能.3.怎样判定这块木板能否通过木框?求出斜边的长,与木板的宽比较.探究新知小于AC即可.17.1勾股定理/解:在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=12+22=5.AC=≈2.24.因为AC大于木板的宽2.2m,所以木板能从门框内通过.5探究新知17.1勾股定理/如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A,B两点间的距离(结果取整数).解:巩固练习22ABBCAC222060240≈57(m).17.1勾股定理/如图,一架2.6米长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4米.(1)求梯子的底端B距墙角O多少米?(2)如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?知识点2勾股定理解决线段移动问题探究新知17.1勾股定理/CODBA(2)在Rt△COD中,根据勾股定理,OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.解:(1)在Rt△AOB中,根据勾股定理,OB2=AB2-OA2=2.62-2.42=1.OB=1.探究新知答:梯子的底端B距墙角O为1米.答:梯子底端B也外移约0.77米.3.151.77,OD1.7710.77.BDODOB17.1勾股定理/我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题.译:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.这个水池的深度与这根芦苇的长度分别是多少?ABC巩固练习17.1勾股定理/ABC解:设AB=x,则AC=x+1,有AB2+BC2=AC2,可列方程,得x2+52=(x+1)2,解方程得x=12.因此x+1=13巩固练习答:这个水池的深度是12尺,这根芦苇的长度是13尺.17.1勾股...