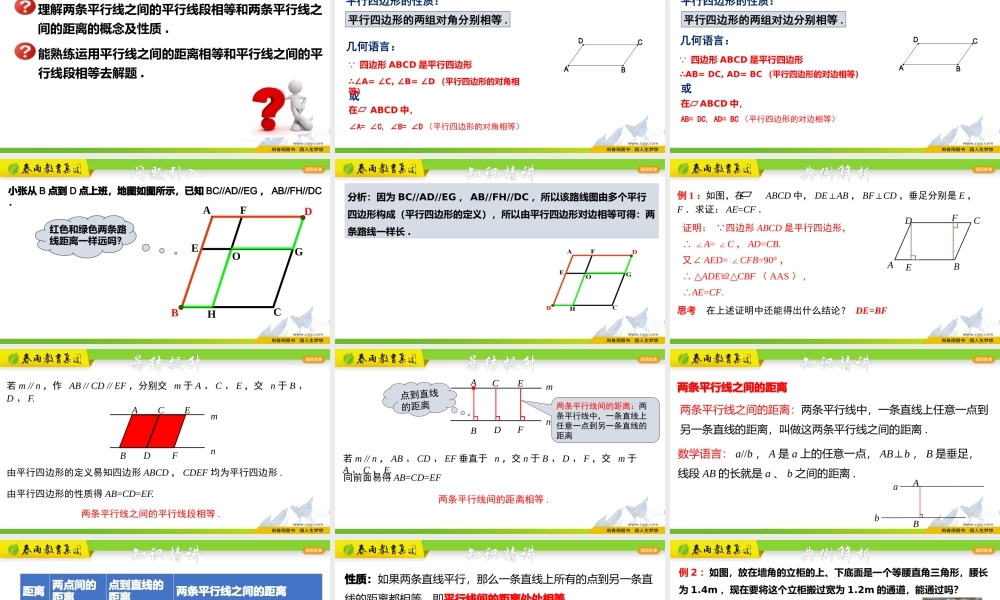
学习目标理解两条平行线之间的平行线段相等和两条平行线之间的距离的概念及性质.能熟练运用平行线之间的距离相等和平行线之间的平行线段相等去解题.几何语言:DACB 四边形ABCD是平行四边形在ABCD中,或∴∠A=∠C,∠B=∠D(平行四边形的对角相等)∠A=∠C,∠B=∠D(平行四边形的对角相等)平行四边形的两组对角分别相等.复习回顾平行四边形的性质:几何语言:DACB 四边形ABCD是平行四边形在ABCD中,或∴AB=DC,AD=BC(平行四边形的对边相等)AB=DC,AD=BC(平行四边形的对边相等)平行四边形的两组对边分别相等.平行四边形的性质:复习回顾OABDEGFHC小张从B点到D点上班,地图如图所示,已知BC//AD//EG,AB//FH//DC.红色和绿色两条路线距离一样远吗?问题引入分析:因为BC//AD//EG,AB//FH//DC,所以该路线图由多个平行四边形构成(平行四边形的定义),所以由平行四边形对边相等可得:两条路线一样长.知识精讲例1:如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.证明: 四边形ABCD是平行四边形,∴∠A=∠C,AD=CB.又∠AED=∠CFB=90°,∴△ADE≌△CBF(AAS),∴AE=CF.思考在上述证明中还能得出什么结论?DABCFEDE=BF典例解析CBFEAD若m//n,作AB//CD//EF,分别交m于A、C、E,交n于B、D、F.由平行四边形的性质得AB=CD=EF.两条平行线之间的平行线段相等.mn由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.总结提升两条平行线间的距离相等.若m//n,AB、CD、EF垂直于n,交n于B、D、F,交m于A、C、E.BFEAnmCD点到直线的距离同前面易得AB=CD=EF两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离总结提升两条平行线之间的距离两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.数学语言:a//b,A是a上的任意一点,AB⊥b,B是垂足,线段AB的长就是a、b之间的距离.abA┐B知识精讲距离两点间的距离点到直线的距离两条平行线之间的距离区别联系连接两点的线段的长度点到直线的垂线段的长度两条平行线中,从一条直线上任一点到另一条直线的垂线段的长度都是指某一条线段的长度知识精讲性质:如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.数学语言:如图所示,A、C是直线l1上的任意两点.l1l2AB┐┐CD l1//l2,AB⊥l2,CD⊥l2,∴AB=CD.知识精讲例2:如图,放在墙角的立柜的上、下底面是一个等腰直角三...