6.1 平行四边形及其性质（2）.pptxVIP免费

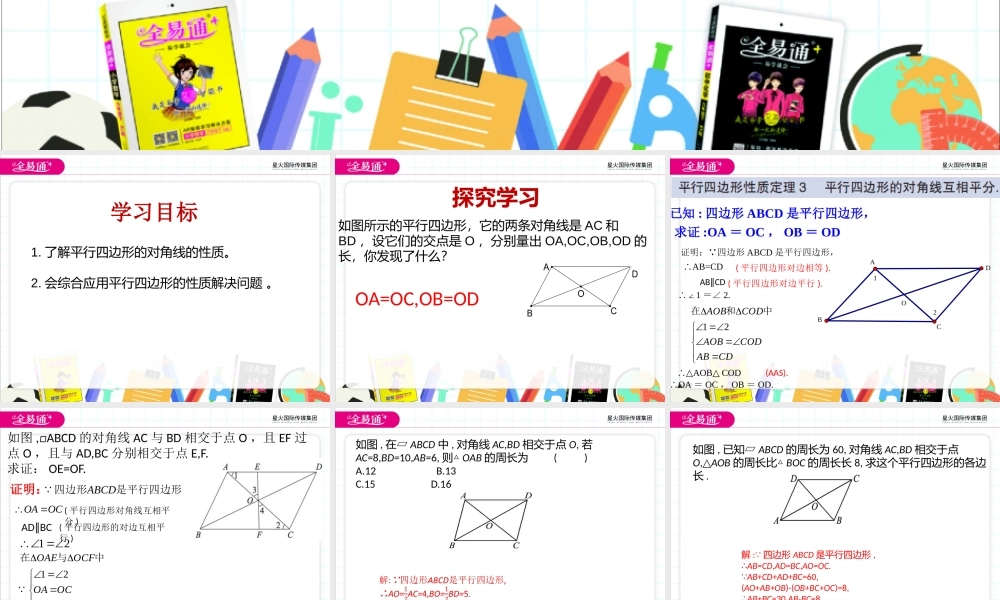
6.1平行四边形及其性质（2）1.了解平行四边形的对角线的性质。2.会综合应用平行四边形的性质解决问题。学习目标如图所示的平行四边形，它的两条对角线是AC和BD，设它们的交点是O，分别量出OA,OC,OB,OD的长，你发现了什么？OA=OC,OB=ODODACB探究学习证明：∵四边形ABCD是平行四边形，∴AB=CD∴∠1＝∠2.∴△AOBCOD△∴OA＝OC，OB＝OD.已知:四边形ABCD是平行四边形，求证:OA＝OC，OB＝ODO21DCBA(AAS).CDABCODAOBCODAOB21中和在ABCD∥(平行四边形对边相等).(平行四边形对边平行).如图,□ABCD的对角线AC与BD相交于点O，且EF过点O，且与AD,BC分别相交于点E,F.求证：OE=OF.证明：4321OCOAOCFOAE中与在12ABCD四边形是平行四边形(平行四边形对角线互相平分)ADBC∥(平行四边形的对边互相平行)OAOCOAEOCF=OEOF(ASA)如图,在▱ABCD中,对角线AC,BD相交于点O,若AC=8,BD=10,AB=6,则△OAB的周长为()A.12B.13C.15D.16如图,已知▱ABCD的周长为60,对角线AC,BD相交于点O,△AOB的周长比△BOC的周长长8,求这个平行四边形的各边长.解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AO=OC.∵AB+CD+AD+BC=60,(AO+AB+OB)-(OB+BC+OC)=8,∴AB+BC=30,AB-BC=8.∴AB=CD=19,BC=AD=11.平行四边形的一条边长是14cm,它的两条对角线长可以是()A.12cm,16cmB.20cm,22cmC.10cm,16cmD.14cm,12cm(江苏泰州中考)如图,▱ABCD中,AC,BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为.如图,在▱ABCD中,对角线AC,BD相交于点O,过点O作直线EF,分别交AD,BC于点E,F.试判断四边形ABFE的面积与四边形FCDE的面积有何关系,并说明理由.解:S四边形ABFE=S四边形FCDE.理由如下:∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC.∴1∠=2∠.又∵∠3=4,∠∴△AOE≌△COF.S∴△AOE=S△COF.∴S四边形ABFE=S△ABC-S△COF+S△AOE=S△ABC,S四边形FCDE=S△CDA-S△AOE+S△COF=S△CDA.∵四边形ABCD是平行四边形,∴AB=CD,BC=DA,∠ABC=∠CDA.∴△ABC≌△CDA.S∴△ABC=S△CDA.∴S四边形ABFE=S四边形FCDE.平行四边形有哪些性质？小结