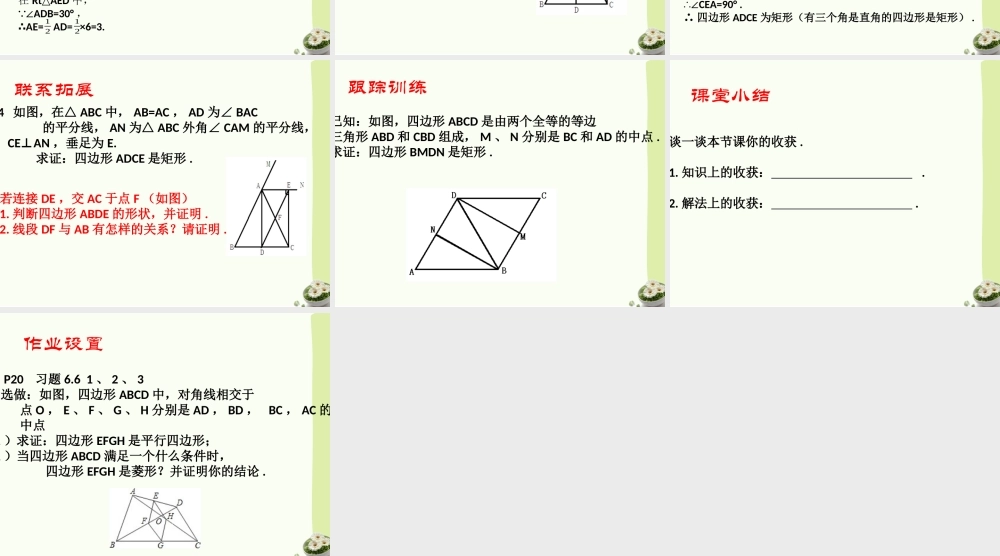
矩形的性质与判定(三)温故知新1.∵四边形ABCD是矩形∴..图中特殊的三角形有.2.∵.∴四边形ABCD是矩形3.如图1,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5cm,则∠DAO=,AC=cm,=_______。ABCDS矩形学习目标1.能够运用综合法和严密的数学语言证明矩形的性质和判定定理以及其他相关结论;2.经历探索、猜测、证明的过程,发展推理论证能力,培养寻找解题思路的能力.自主探究例3如图,在矩形ABCD中,AD=6,对角线AC与BD交于点O,AEBD⊥,垂足为E,ED=3BE.求AE的长.自主探究解∵四边形ABCD是矩形,∴AO=BO=DO=BD(矩形的对角线相等且互相平分).∠BAD=90°(矩形的四个都是直角).∵ED=3BE,∴BE=OE.又∵AEBD⊥,∴AB=AO.∴AB=AO=BO.即△ABO是等边三角形.∴∠ABO=60°.∴∠ADB=90°-ABO=30°.∠在RtAED△中,∵∠ADB=30°,∴AE=AD=×6=3.121212例4如图,在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.合作探究证明:∵AD平分∠BAC,AN平分∠CAM,∴∠CAD=∠BAC,∠CAN=∠CAM.∴∠DAE=∠CAD+∠CAN=(∠BAC=∠CAM)=×180°=90°.在△ABC中,∵AB=AC,AD为∠BAC的平分线,∴AD⊥BC.∴∠ADC=90°.又∵CE⊥AN,∴∠CEA=90°.∴四边形ADCE为矩形(有三个角是直角的四边形是矩形).合作探究121212124如图,在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.联系拓展若连接DE,交AC于点F(如图)1.判断四边形ABDE的形状,并证明.2.线段DF与AB有怎样的关系?请证明.跟踪训练已知:如图,四边形ABCD是由两个全等的等边三角形ABD和CBD组成,M、N分别是BC和AD的中点.求证:四边形BMDN是矩形.课堂小结谈一谈本节课你的收获.1.知识上的收获:.2.解法上的收获:.作业设置P20习题6.61、2、3选做:如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点1)求证:四边形EFGH是平行四边形;2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论.