28.1 锐角三角函数（第3课时）.docxVIP免费

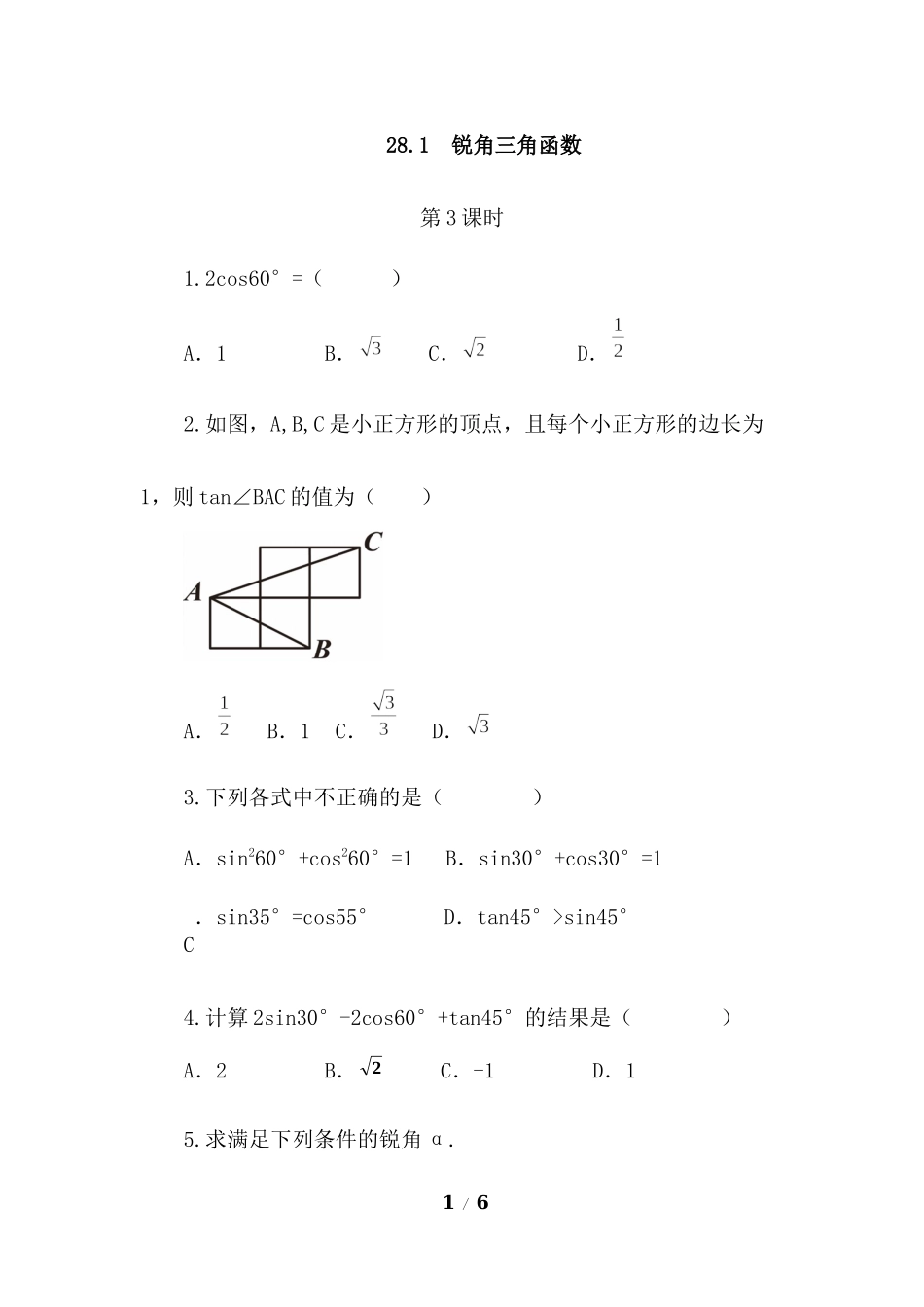
1/628.1锐角三角函数第3课时1.2cos60°=（）A．1B．C．D．2.如图，A,B,C是小正方形的顶点，且每个小正方形的边长为1，则tan∠BAC的值为（）A．B．1C．D．3.下列各式中不正确的是（）A．sin260°+cos260°=1B．sin30°+cos30°=1C．sin35°=cos55°D．tan45°>sin45°4.计算2sin30°-2cos60°+tan45°的结果是（）A．2B．2C．-1D．15.求满足下列条件的锐角α.2/6(1)2sinα－=0；(2)tanα－1=0.6.在△ABC中，∠A,∠B都是锐角，且22sinA，23cosB，则△ABC的形状是（）A.直角三角形B.钝角三角形C.锐角三角形D.不能确定7.在△ABC中，若，则∠C=.8.求下列各式的值：(1)1－2sin30°cos30°；(2)3tan30°－tan45°+2sin60°；(3)；(4)3/69.已知α为锐角，且tanα是方程x2+2x－3=0的一个根，求2sin2α+cos2α－tan(α+15°)的值．4/610.如图，在△ABC中，AD⊥BC，M为AB的中点，∠B=30°，22cosACD.求tan∠BCM.参考答案：1.A5/62.解：原式＝1＋3－1－=.3.B4.D5.解：⑴23sina，∴∠α=60°.⑵tanα=1，∴∠α=45°.6.B7.120°8.答案：(1)1-；⑵⑶2；⑷9.解：解方程x2+2x－3=0，得x1=1，x2=－3.∵tanα＞0，∴tanα=1，∴α=45°.∴2sin2α+cos2α－tan(α+15°)=2sin245°+cos245°－tan60°6/6=10.解：过点M作ME⊥BC于点E.∵AD⊥BC，,22cosACD∴CD=AD,又∵M是AB的中点，∴BE=DE，AD=2ME.又∵∠B=30°，∴∴∴