28.1 锐角三角函数（第2课时）.pptxVIP免费

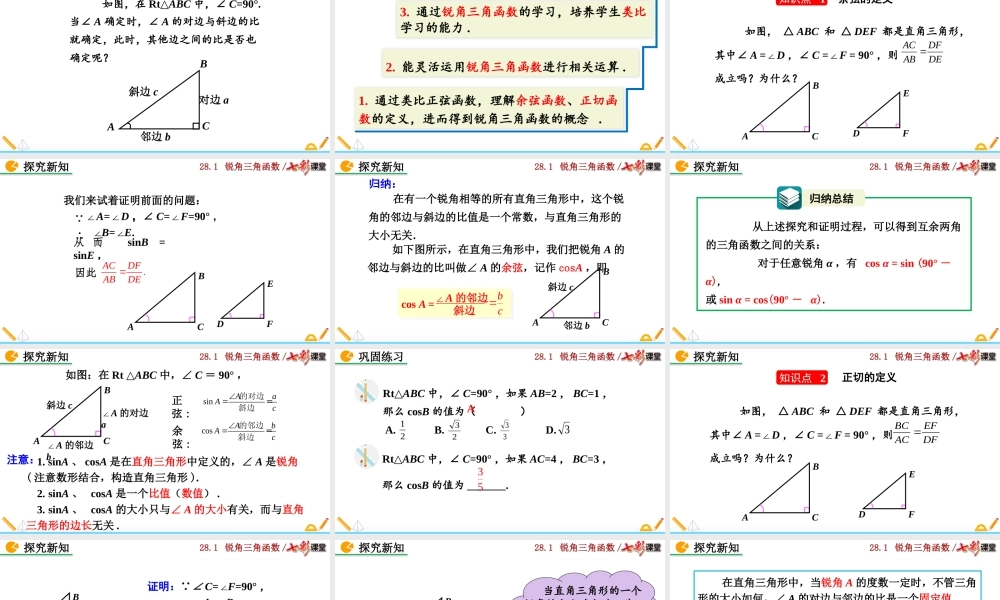
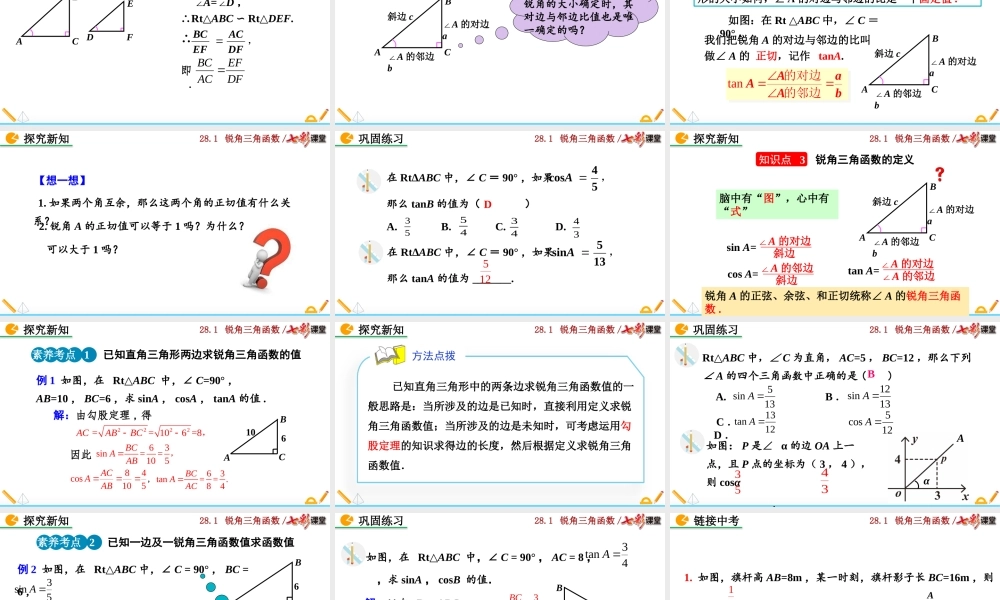
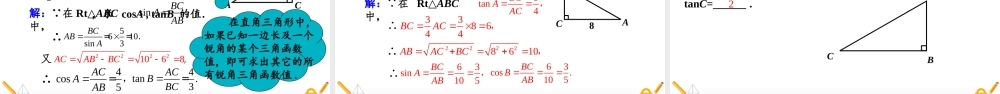28.1锐角三角函数/28.1锐角三角函数(第2课时)人教版数学九年级下册28.1锐角三角函数/如图，在Rt△ABC中，∠C=90°.ACB对边a邻边b斜边c当∠A确定时，∠A的对边与斜边的比就确定，此时，其他边之间的比是否也确定呢？导入新知28.1锐角三角函数/2.能灵活运用锐角三角函数进行相关运算.1.通过类比正弦函数，理解余弦函数、正切函数的定义，进而得到锐角三角函数的概念.素养目标3.通过锐角三角函数的学习，培养学生类比学习的能力.28.1锐角三角函数/如图，△ABC和△DEF都是直角三角形，其中∠A=∠D，∠C=∠F=90°，则成立吗？为什么？DEDFABACABCDEF探究新知知识点1余弦的定义28.1锐角三角函数/我们来试着证明前面的问题： ∠A=∠D，∠C=∠F=90°，∴∠B=∠E.从而sinB=sinE，因此.ACDFABDEABCDEF探究新知28.1锐角三角函数/在有一个锐角相等的所有直角三角形中，这个锐角的邻边与斜边的比值是一个常数，与直角三角形的大小无关．如下图所示，在直角三角形中，我们把锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA，即归纳：ABC斜边c邻边b探究新知∠A的邻边斜边cosA=bc28.1锐角三角函数/探究新知归纳总结从上述探究和证明过程，可以得到互余两角的三角函数之间的关系：对于任意锐角α，有cosα=sin(90°－α),或sinα=cos(90°－α).28.1锐角三角函数/1.sinA、cosA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形).2.sinA、cosA是一个比值（数值）.3.sinA、cosA的大小只与∠A的大小有关，而与直角三角形的边长无关.如图：在Rt△ABC中，∠C＝90°，正弦:余弦:sin的对边=斜边AaAccos的邻边=斜边AbAc探究新知注意：ABC斜边c∠A的邻边b∠A的对边a28.1锐角三角函数/Rt△ABC中，∠C=90°，如果AB=2，BC=1，那么cosB的值为（）A.B.C.D.2333321A巩固练习Rt△ABC中，∠C=90°，如果AC=4，BC=3，那么cosB的值为_______.3528.1锐角三角函数/如图，△ABC和△DEF都是直角三角形，其中∠A=∠D，∠C=∠F=90°，则成立吗？为什么？DFEFACBCABCDEF探究新知知识点2正切的定义28.1锐角三角函数/证明： ∠C=F=∠90°，∠A=D∠，∴Rt△ABCRt∽△DEF.探究新知ABCDEF，DFACEFBC∴即.DFEFACBC28.1锐角三角函数/当直角三角形的一个锐角的大小确定时，其对边与邻边比值也是唯一确定的吗？探究新知ABC斜边c∠A的邻边b∠A的对边a28.1锐角三角函数/如图：在Rt△ABC中，∠C＝90°，我们把锐角A的对边与邻边的比叫做∠A的正切，记作tanA.tan的对边...