高中数学 3.1直线的倾斜角与斜率课件2 新人教A版必修2.pptVIP免费

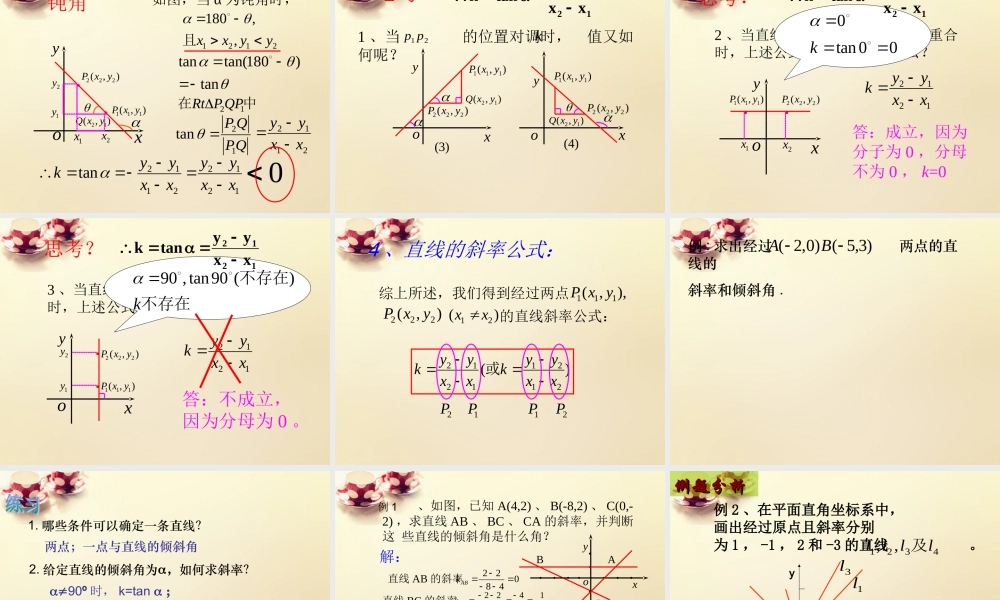
X.pYO一、直线的倾斜角1、直线倾斜角的定义：当直线l与x轴相交时，我们取x轴作为基准，x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角.yxol下列四图中，表示直线的倾斜角的是()练习：yxoAyxoByxoCyxoDA2、直线倾斜角的范围：当直线与轴平行或重合时，我们规定它的倾斜角为，因此，直线的倾斜角的取值范围为：00180xlyxo零度角yxo锐角yxo直角yxo钝角按倾斜角去分类，直线可分几类？3、直线倾斜角的意义体现了直线对x轴正方向的倾斜程度在平面直角坐标系中，每一条直线都有一个确定的倾斜角。倾斜角倾斜程度2l3lx1lyo倾斜角能确定一条直线吗？相同倾斜角可作无数互相平行的直线4、如何才能确定直线位置？yxo一点+倾斜角确定一条直线过一点且倾斜角为能不能确定一条直线？（两者缺一不可）能l在同一个坐标系中画出过原点并且倾斜角分别是1354530000,,的直线,试着写出它们的直线方程.然后观察思考:直线的倾斜角在直线方程中是如何体现出来的??xyxyxy135453000033系数是倾斜角正切值定义:倾斜角不是的直线,它的倾斜角的正切叫做这条直线的斜率.记作,即900ktank倾斜角为的直线没有斜率.900练习:指出下列直线的倾斜角和斜率.025tanxy)4(x33y)3(x3y)2(x3y)1(问题3:已知两个点如何求斜率？3、探究：由两点确定的直线的斜率),(111yxP),(222yxP212112,,yyxxQPP且如图，当α为锐角时，能不能构造一个直角三角形去求？tankxyo1x2x1y2y),(12yxQ中在QPPRt12QPQPQPPk1212tantan1212xxyy0锐角xyo),(111yxP),(222yxP),(12yxQ如图，当α为钝角时，2121,,180yyxx且tan)180tan(tan中在12QPPRtQPQP12tan2112xxyy12122112tanxxyyxxyyk01x2x1y2y钝角思考？xyo(3)),(12yxQ),(111yxP),(222yxPyox(4)),(12yxQ),(111yxP),(222yxP21pp1、当的位置对调时，值又如何呢？k1212xxyytank思考？2、当直线平行于x轴，或与x轴重合时，上述公式还适用吗？为什么？xyo),(111yxP),(222yxP1x2x1212xxyyk00tan0k答：成立，因为分子为0，分母不为0，k=01212xxyytank3、当直线平行于y轴，或与y轴重合时，上述公式还适用吗？为什么？xyo),(111yxP),(222yxP1y2y1212xxyyk思考？不存在不存在k)(90tan,90答：不成立，因为分母为0。1212xxyyta...