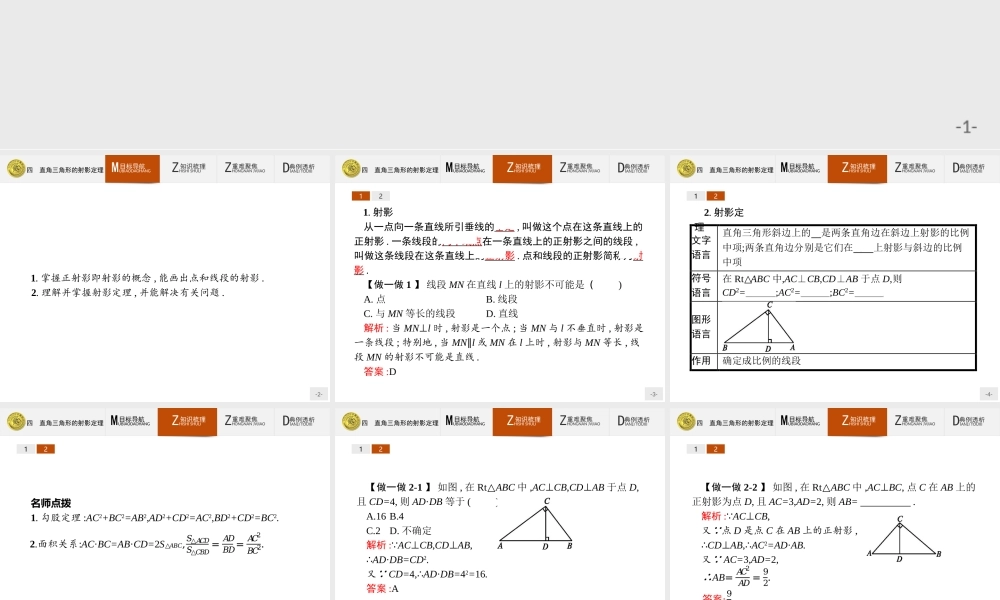
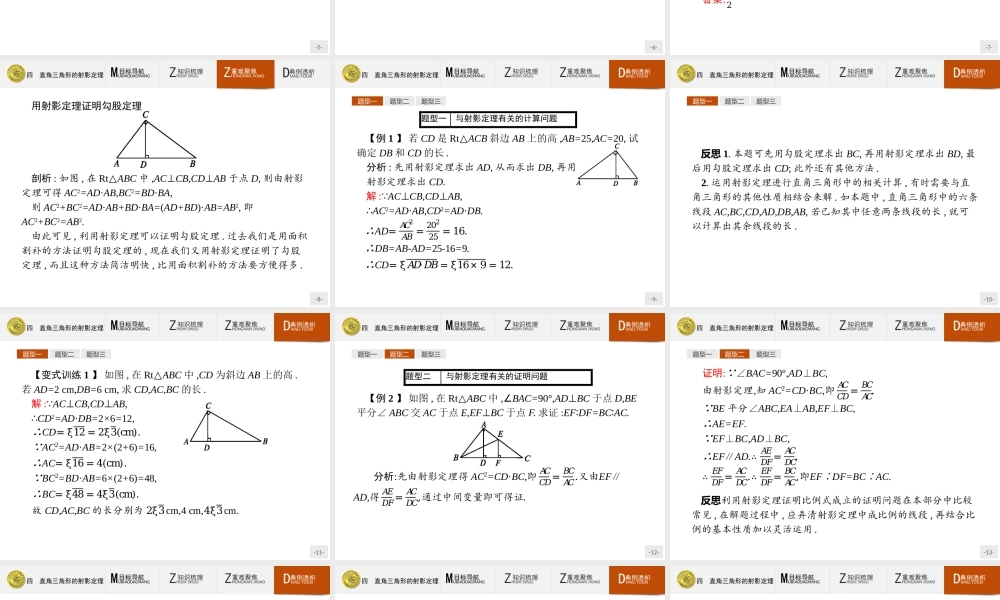
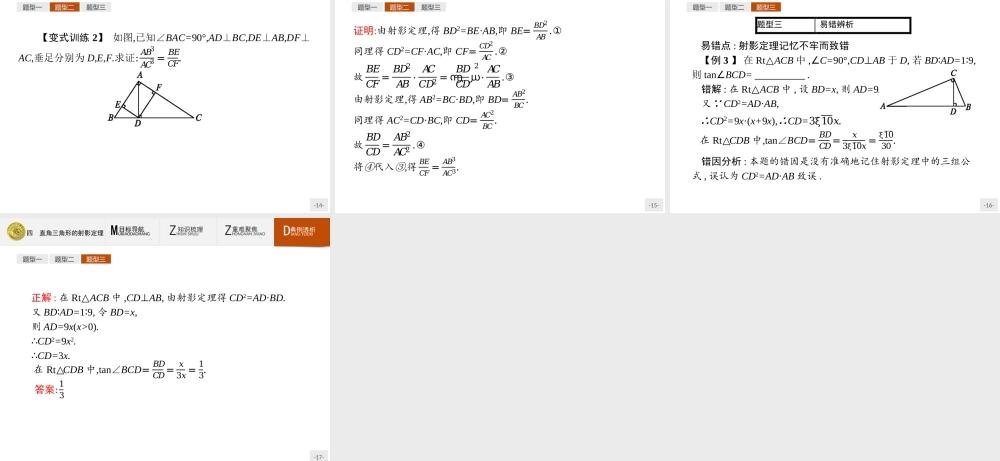
-1-四直角三角形的射影定理-2-四直角三角形的射影定理ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航1.掌握正射影即射影的概念,能画出点和线段的射影.2.理解并掌握射影定理,并能解决有关问题.-3-四直角三角形的射影定理ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航121.射影从一点向一条直线所引垂线的垂足,叫做这个点在这条直线上的正射影.一条线段的两个端点在一条直线上的正射影之间的线段,叫做这条线段在这条直线上的正射影.点和线段的正射影简称为射影.【做一做1】线段MN在直线l上的射影不可能是()A.点B.线段C.与MN等长的线段D.直线解析:当MN⊥l时,射影是一个点;当MN与l不垂直时,射影是一条线段;特别地,当MN∥l或MN在l上时,射影与MN等长,线段MN的射影不可能是直线.答案:D-4-四直角三角形的射影定理ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航122.射影定理文字语言直角三角形斜边上的高是两条直角边在斜边上射影的比例中项;两条直角边分别是它们在斜边上射影与斜边的比例中项符号语言在Rt△ABC中,AC⊥CB,CD⊥AB于点D,则CD2=BD·AD;AC2=AD·AB;BC2=BD·BA图形语言作用确定成比例的线段-5-四直角三角形的射影定理ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航12名师点拨1.勾股定理:AC2+BC2=AB2,AD2+CD2=AC2,BD2+CD2=BC2.2.面积关系:AC·BC=AB·CD=2S△ABC,𝑆△𝐴𝐶𝐷𝑆△𝐶𝐵𝐷=𝐴𝐷𝐵𝐷=𝐴𝐶2𝐵𝐶2.-6-四直角三角形的射影定理ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航12【做一做2-1】如图,在Rt△ABC中,AC⊥CB,CD⊥AB于点D,且CD=4,则AD·DB等于()A.16B.4C.2D.不确定解析: AC⊥CB,CD⊥AB,∴AD·DB=CD2.又 CD=4,∴AD·DB=42=16.答案:A-7-四直角三角形的射影定理ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航12【做一做2-2】如图,在Rt△ABC中,AC⊥BC,点C在AB上的正射影为点D,且AC=3,AD=2,则AB=.解析: AC⊥CB,又 点D是点C在AB上的正射影,∴CD⊥AB,∴AC2=AD·AB.又 AC=3,AD=2,∴AB=𝐴𝐶2𝐴𝐷=92.答案:92-8-四直角三角形的射影定理ZHISHISHULI知识梳理ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航用射影定理证明勾股定理剖析:如图,在Rt△ABC中,AC⊥CB,CD⊥AB于点D,则由射影定...