【数学】2.4.2《抛物线的几何性质》课件（新人教A版选修2-1）.pptVIP免费

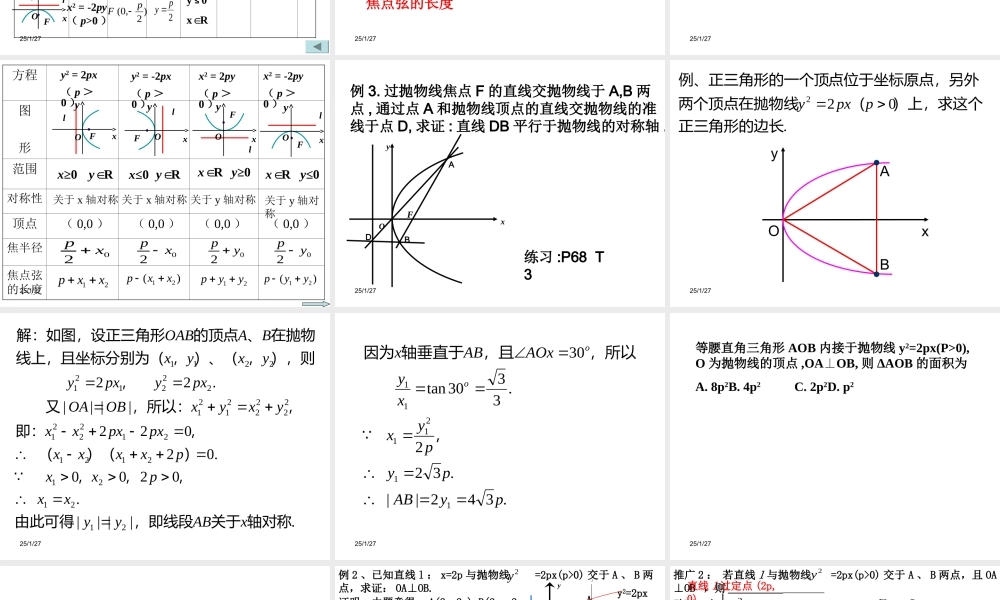
25/1/27抛物线的几何性质25/1/27结合抛物线y2=2px(p>0)的标准方程和图形,探索其的几何性质:(1)范围(2)对称性(3)顶点类比探索x≥0,yR∈关于x轴对称,对称轴又叫抛物线的轴.抛物线和它的轴的交点.25/1/27(4)离心率(5)焦半径(6)通径始终为常数1通过焦点且垂直对称轴的直线，与抛物线相交于两点，连接这两点的线段叫做抛物线的通径。|PF|=x0+p/2xOyFP通径的长度：2P思考：通径是抛物线的焦点弦中最短的弦吗？25/1/27特点1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的,为1;5.抛物线标准方程中的p对抛物线开口的影响.P越大,开口越开阔25/1/27图形方程焦点准线范围顶点对称轴elFyxOlFyxOlFyxOlFyxOy2=2px（p>0）y2=-2px（p>0）x2=2py（p>0）x2=-2py（p>0）)0,2(pF)0,2(pF)2,0(pF)2,0(pF2px2px2py2pyx≥0yR∈x≤0yR∈y≥0xR∈y≤0xR∈(0,0)x轴y轴125/1/27例题例1.顶点在坐标原点,对称轴是坐标轴,并且过点M(2,)的抛物线有几条,求它的标准方程,22例2.斜率为1的直线L经过抛物线的焦点F,且与抛物线相交于A,B两点,求线段AB的长.当焦点在x(y)轴上,开口方向不定时,设为y2=2mx(m≠0)(x2=2my(m≠0)),可避免讨论y2=4x焦点弦的长度25/1/27练习:1.过抛物线的焦点,作倾斜角为的直线,则被抛物线截得的弦长为y2=8x2.过抛物线的焦点做倾斜角为的直线L,设L交抛物线于A,B两点,(1)求|AB|;(2)求|AB|的最小值.04525/1/27方程图形范围对称性顶点焦半径焦点弦的长度y2=2px（p＞0）y2=-2px（p＞0）x2=2py（p＞0）x2=-2py（p＞0）lFyxOlFyxOlFyxOx≥0yR∈x≤0yR∈xR∈y≥0y≤0xR∈lFyxO12pxx12()pxx12pyy12()pyy02px02px02py02py关于x轴对称关于x轴对称关于y轴对称关于y轴对称（0,0）（0,0）（0,0）（0,0）25/1/27例3.过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.xOyFABD练习:P68T325/1/27.022正三角形的边长）上，求这个（两个顶点在抛物线点位于坐标原点，另外例、正三角形的一个顶ppxyyOxBA25/1/27.||||.0200.02022||||.222121212121212221222221212221212211轴对称关于，即线段由此可得，，，））（（，即：，，所以：又，），则，）、（，线上，且坐标分别为（在抛物、的顶点解：如图，设正三角形xAByyxxpxxpxxxxpxpxxxy...