28.1 第2课时 余弦函数和正切函数.pptVIP免费

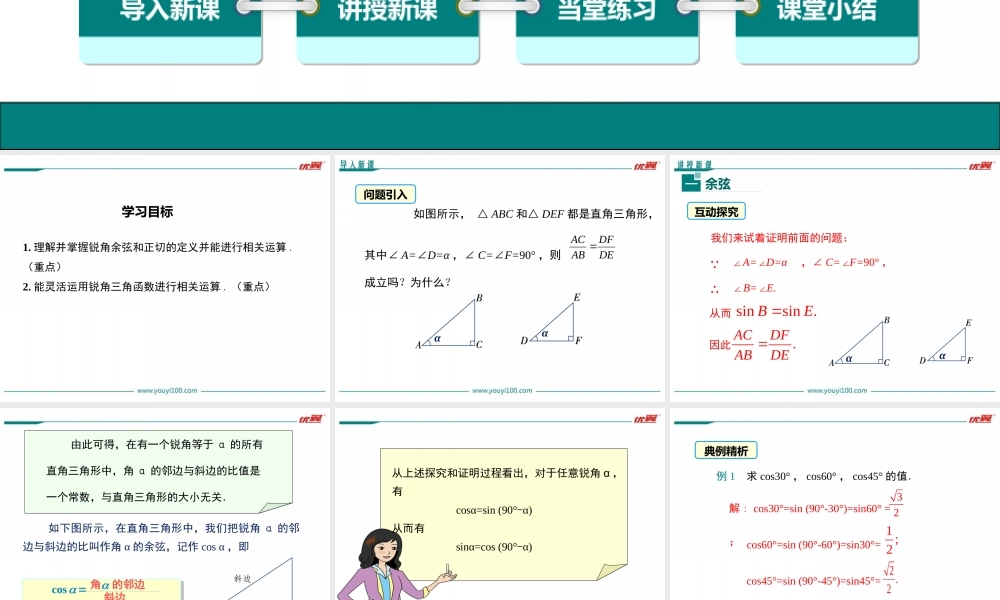
优翼课件导入新课讲授新课当堂练习课堂小结学练优九年级数学下（RJ）教学课件28.1锐角三角函数第二十八章锐角三角函数第2课时余弦函数和正切函数学习目标1.理解并掌握锐角余弦和正切的定义并能进行相关运算.（重点）2.能灵活运用锐角三角函数进行相关运算.（重点）导入新课问题引入如图所示，△ABC和△DEF都是直角三角形，其中∠A=∠D=α，∠C=∠F=90°，则成立吗？为什么？ααDEDFABAC讲授新课余弦一互动探究我们来试着证明前面的问题： ∠A=∠D=α，∠C=∠F=90°，∴∠B=∠E.αα从而sinsin.BE因此.ACDFABDE由此可得，在有一个锐角等于α的所有直角三角形中，角α的邻边与斜边的比值是一个常数，与直角三角形的大小无关．如下图所示，在直角三角形中，我们把锐角α的邻边与斜边的比叫作角α的余弦，记作cosα，即斜边cos角的邻边α从上述探究和证明过程看出，对于任意锐角α，有cosα=sin(90°-α)从而有sinα=cos(90°-α)例1求cos30°，cos60°，cos45°的值．32解:cos30°=sin(90°-30°)=sin60°=；cos60°=sin(90°-60°)=sin30°=1;2cos45°=sin(90°-45°)=sin45°=2.2典例精析例2如图，AB为⊙O的直径，且弦CDAB⊥于E，过点B的切线与AD的延长线交于点F．若cosC=∠，DF=3，求⊙O的半径．45解析：由于∠A、∠C所对的弧相同，因此cosA=cosC，由此可得BF、AF、AB的比例关系，可用未知数表示出它们的长．连接BD，易证△BDFABF∽△，根据所得比例线段即可求得未知数的值，从而得到直径AB的长，从而得到⊙O的半径．解：连接BD．在⊙O中，∠C=A∠， BF是⊙O的切线，∴∠ABF=90°．设AB=4x，则AF=5x，由勾股定理得，BF=3x． AB是⊙O的直径，∴BDAD⊥，∴cosA=cosC=4.5∴△ABFBDF∽△，BFDF=AFBF，33=53xxx即，5.3x解得⊙O的半径为110AB2.23x1.如图，在平面直角坐标系中，点A的坐标为（4，3），那么cosα的值是（）34A.43B.35C.45D.练一练D2.如图，在Rt△ABC中，斜边AB的长为m，∠A=35°，则直角边BC的长是（）sin35mA.cos35mB.cos35mC.cos35mD.A正切二我们已经知道，在直角三角形中，当一个锐角的大小确定时，那么不管这个三角形的大小如何，这个锐角的对边（或邻边）与斜边的比值也就确定（是一个常数）.那么这个锐角的对边与邻边的比值是否也是一个常数呢？想一想问题如图，△ABC和△DEF都是直角三角形，其中∠A=∠D=α，∠C=∠F=90°，则成立吗？为什么？DFEFACBCαα∴Rt△ABCRt∽△DEF.即BC...