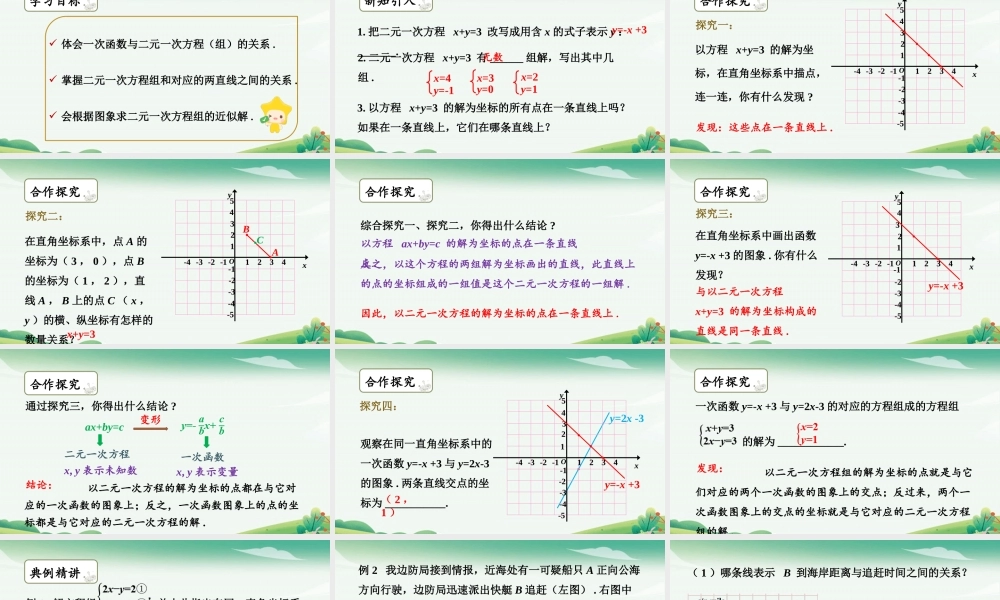
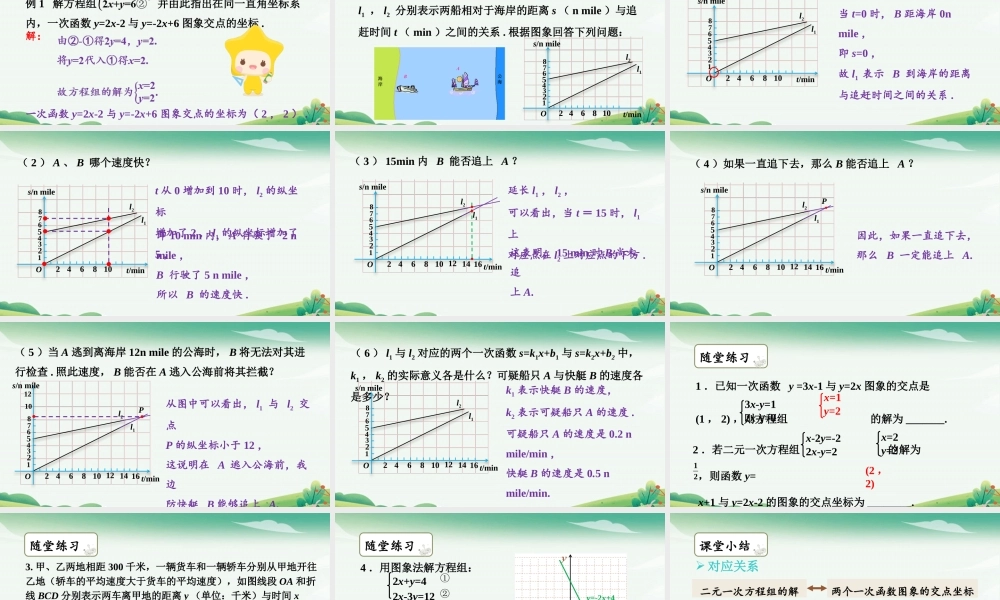
5.5一次函数的简单应用第2课时一次函数与二元一次方程组学习目标体会一次函数与二元一次方程(组)的关系.掌握二元一次方程组和对应的两直线之间的关系.会根据图象求二元一次方程组的近似解.新知引入1.把二元一次方程x+y=3改写成用含x的式子表示y:_______.3.以方程x+y=3的解为坐标的所有点在一条直线上吗?如果在一条直线上,它们在哪条直线上?y=-x+32.二元一次方程x+y=3有______组解,写出其中几组.无数x=4y=-1x=3y=0x=2y=1合作探究O4312yx23451-1-2-4-3-4-3-2-1-5以方程x+y=3的解为坐标,在直角坐标系中描点,连一连,你有什么发现?发现:这些点在一条直线上.探究一:合作探究在直角坐标系中,点A的坐标为(3,0),点B的坐标为(1,2),直线A,B上的点C(x,y)的横、纵坐标有怎样的数量关系?探究二:x+y=3O4312yx23451-1-2-4-3-4-3-2-1-5ABC合作探究综合探究一、探究二,你得出什么结论?以方程ax+by=c的解为坐标的点在一条直线上.反之,以这个方程的两组解为坐标画出的直线,此直线上的点的坐标组成的一组值是这个二元一次方程的一组解.因此,以二元一次方程的解为坐标的点在一条直线上.合作探究探究三:O4312yx23451-1-2-4-3-4-3-2-1-5在直角坐标系中画出函数y=-x+3的图象.你有什么发现?y=-x+3与以二元一次方程x+y=3的解为坐标构成的直线是同一条直线.合作探究通过探究三,你得出什么结论?ax+by=c变形二元一次方程x,y表示未知数一次函数x,y表示变量结论:以二元一次方程的解为坐标的点都在与它对应的一次函数的图象上;反之,一次函数图象上的点的坐标都是与它对应的二元一次方程的解.合作探究探究四:观察在同一直角坐标系中的一次函数y=-x+3与y=2x-3的图象.两条直线交点的坐标为___________.O4312yx23451-1-2-4-3-4-3-2-1-5y=-x+3y=2x-3(2,1)合作探究一次函数y=-x+3与y=2x-3的对应的方程组成的方程组的解为____________.以二元一次方程组的解为坐标的点就是与它们对应的两个一次函数的图象上的交点;反过来,两个一次函数图象上的交点的坐标就是与它对应的二元一次方程组的解.发现:典例精讲例1解方程组并由此指出在同一直角坐标系内,一次函数y=2x-2与y=-2x+6图象交点的坐标.解:一次函数y=2x-2与y=-2x+6图象交点的坐标为(2,2).例2我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(左图).右图中l1,l2分别表示两船相对于海岸的距离s(nmile)与追赶时间t(min)之间的关系.根据图象回...