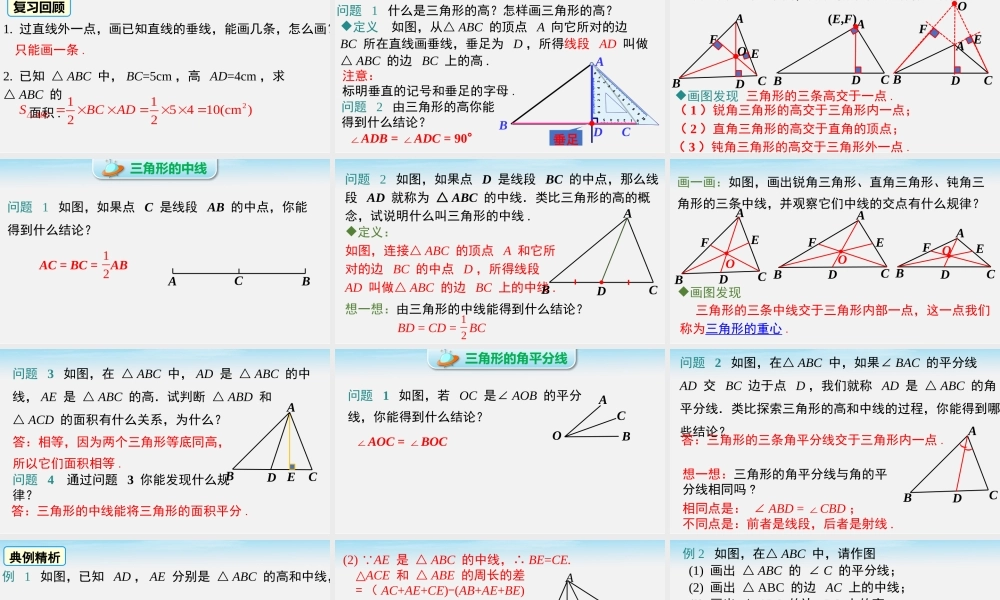
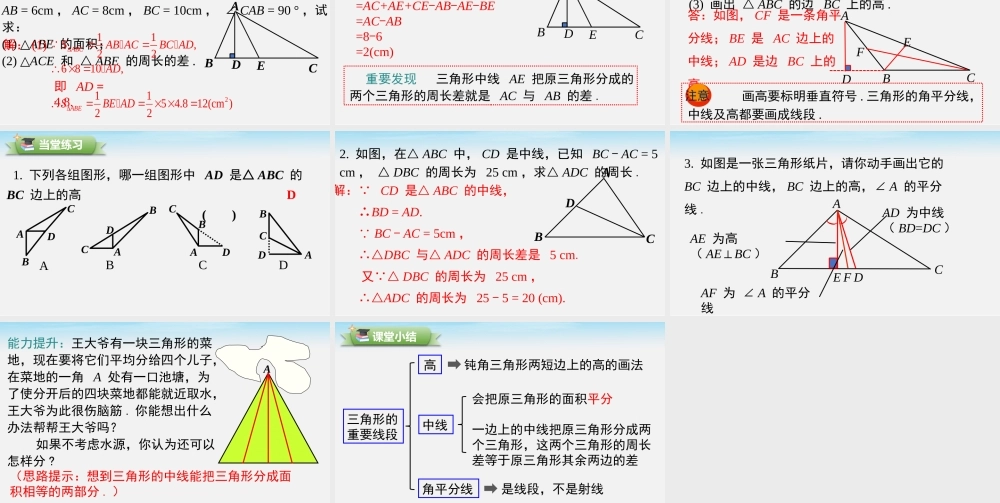
优翼9.1三角形9.1.1认识三角形第2课时三角形中的重要线段导入新课复习回顾1.过直线外一点,画已知直线的垂线,能画几条,怎么画?只能画一条.2.已知△ABC中,BC=5cm,高AD=4cm,求△ABC的面积.2115410(cm)22ABCSBCAD△新课讲授三角形的高问题1什么是三角形的高?怎样画三角形的高?定义如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.问题2由三角形的高你能得到什么结论?∠ADB=∠ADC=90°ABCD垂足注意:标明垂直的记号和垂足的字母.ABCDEFABCDABCDEF画图发现三角形的三条高交于一点.(1)锐角三角形的高交于三角形内一点;(2)直角三角形的高交于直角的顶点;(3)钝角三角形的高交于三角形外一点.O(E,F)O画一画如图,分别画出锐角三角形、直角三角形、钝角三角形的三条高,并观察高的交点有什么规律?三角形的中线问题1如图,如果点C是线段AB的中点,你能得到什么结论?ACBAC=BC=AB12定义:如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.问题2如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线.ABC想一想:由三角形的中线能得到什么结论?BD=CD=BC12D画一画:如图,画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?画图发现三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.ABCABCABCDEFDDEFEFOOO问题3如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系,为什么?BCDEA答:相等,因为两个三角形等底同高,所以它们面积相等.问题4通过问题3你能发现什么规律?答:三角形的中线能将三角形的面积平分.三角形的角平分线问题1如图,若OC是∠AOB的平分线,你能得到什么结论?ACBO∠AOC=∠BOC想一想:三角形的角平分线与角的平分线相同吗?相同点是:∠ABD=∠CBD;不同点是:前者是线段,后者是射线.问题2如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.类比探索三角形的高和中线的过程,你能得到哪些结论?BCDA((答:三角形的三条角平分线交于三角形内一点.典例精析例1如图,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°,试求:(1)△ABE的面积;(2)△ACE和△ABE的周长的差.ABCDE解:(1)11,226810,ABCSABACBCADAD...