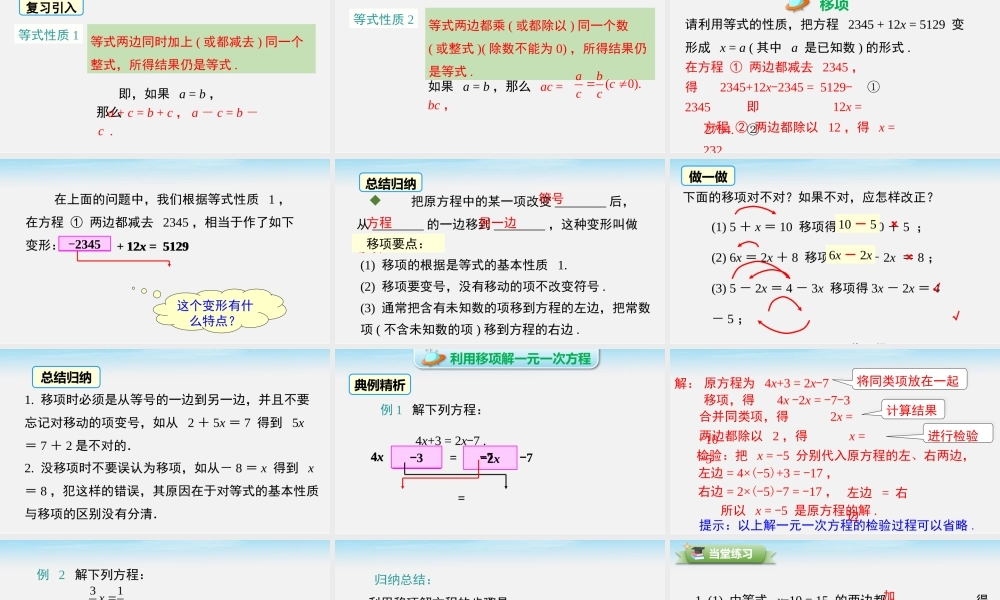
优翼6.2解一元一次方程第2课时方程的简单变形6.2.1等式的性质与方程的简单变形导入新课复习引入等式性质1等式两边同时加上(或都减去)同一个整式,所得结果仍是等式.即,如果a=b,那么a+c=b+c,a-c=b-c.等式两边都乘(或都除以)同一个数(或整式)(除数不能为0),所得结果仍是等式.如果a=b,那么ac=bc,(0).abccc等式性质2新课讲授请利用等式的性质,把方程2345+12x=5129变形成x=a(其中a是已知数)的形式.①在方程①两边都减去2345,得2345+12x-2345=5129-2345即12x=2784.②方程②两边都除以12,得x=232移项+12x=5129234512x=5129-2345在上面的问题中,我们根据等式性质1,在方程①两边都减去2345,相当于作了如下变形:这个变形有什么特点?把原方程中的某一项改变________后,从________的一边移到________,这种变形叫做移项.(1)移项的根据是等式的基本性质1.(2)移项要变号,没有移动的项不改变符号.(3)通常把含有未知数的项移到方程的左边,把常数项(不含未知数的项)移到方程的右边.移项要点:符号方程另一边总结归纳(1)5+x=10移项得x=10+5;(2)6x=2x+8移项得6x+2x=8;(3)5-2x=4-3x移项得3x-2x=4-5;移得做一做××√√10-56x-2x下面的移项对不对?如果不对,应怎样改正?1.移项时必须是从等号的一边到另一边,并且不要忘记对移动的项变号,如从2+5x=7得到5x=7+2是不对的.2.没移项时不要误认为移项,如从-8=x得到x=8,犯这样的错误,其原因在于对等式的基本性质与移项的区别没有分清.总结归纳例1解下列方程:4x+3=2x-7.利用移项解一元一次方程4x+3=2x-74x-2x=-3-7典例精析解:原方程为4x+3=2x-7将同类项放在一起将同类项放在一起合并同类项,得2x=-10移项,得4x-2x=-7-3所以x=-5是原方程的解.检验:把x=-5分别代入原方程的左、右两边,左边=4×(-5)+3=-17,右边=2×(-5)-7=-17,左边=右边计算结果计算结果进行检验进行检验两边都除以2,得x=-5提示:以上解一元一次方程的检验过程可以省略.例2解下列方程:31.23x解:方程两边都除以(或都乘),得322313123233x即2.9x(1)移项;利用移项解方程的步骤是:(3)化未知数的系数为1.(2)合并同类项;归纳总结:当堂练习1.(1)由等式x-10=15的两边都,得到等式x=5,这是根据;(2)由等式的两边都,得到等式x=,这是根据加10等式基本性质1等式基本性质2乘-3981338xD2.方程3x-1=5的解是()A.B.C.x=18D.x=234x53xD3.若关于x的方程2x+a-9=0的解是x=2,则a的值...