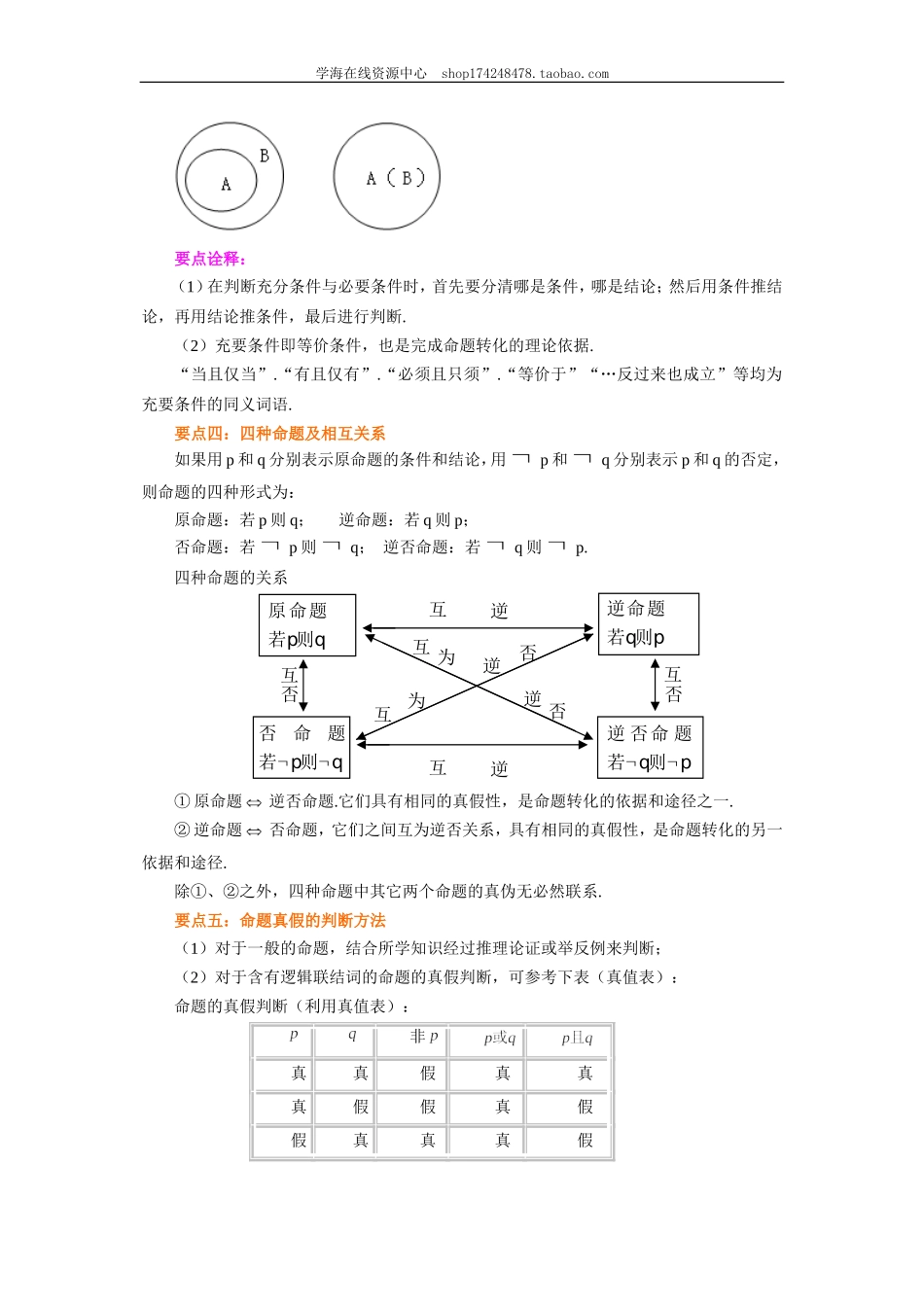
学海在线资源中心shop174248478.taobao.com《常用逻辑用语》全章复习与巩固编稿:李霞审稿:张林娟【学习目标】1.理解命题的概念;了解逻辑联结词“或”、“且”、“非”的含义.2.了解命题“若p,则q”的形式及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.3.理解必要条件、充分条件与充要条件的意义.4.理解全称量词与存在量词的意义;能正确地对含有一个量词的命题进行否定.【知识网络】【要点梳理】要点一:命题(1)命题的概念:可以真假的语句叫做命题.一般可以用小写英文字母表示.其中判断为真的语句叫真命题,判断为假的语句叫假命题.(2)全称量词与全称命题全称量词:在指定范围内,表示整体或者全部的含义的量词称为全称量词.如“所有的”、“任意一个”、“每一个”、“一切”、“任给”等.学海在线资源中心shop174248478.taobao.com全称命题:含有全称量词的命题,叫做全称命题.符号表示为,(3)存在量词与存在性命题存在量词:表示个别或一部分的含义的量词称为存在量词.如“有一个”,“存在一个”,“至少有一个”,“有的”,“有些”等.存在性命题:含有存在量词的命题,叫做存在性命题.符号表示为,.要点二:基本逻辑联结词基本逻辑联结词有“或”、“且”、“非”.(1):用“且”把命题和联结起来,得到的新命题,读作“且”,相当于集合中的交集.(2):用“或”把命题和联结起来,得到的新命题,读作“或”,相当于集合中的并集.(3):对命题加以否定,得到的新命题,读作“非”或“的否定”,相当于集合中的补集.要点三:充分条件、必要条件、充要条件对于“若p则q”形式的命题:①若pq,则p是q的充分条件,q是p的必要条件;②若pq,但qp,则p是q的充分不必要条件,q是p的必要不充分条件;③若既有pq,又有qp,记作pq,则p是q的充分必要条件(充要条件).判断命题充要条件的三种方法(1)定义法:(2)等价法:由于原命题与它的逆否命题等价,否命题与逆命题等价,因此,如果原命题与逆命题真假不好判断时,还可以转化为逆否命题与否命题来判断.即利用与;与;与的等价关系,对于条件或结论是不等关系(或否定式)的命题,一般运用等价法.(3)利用集合间的包含关系判断,比如AB可判断为AB;A=B可判断为AB,且BA,即AB.如图:“”“,且”是的充分不必要条件.“”“”是的充分必要条件.学海在线资源中心shop174248478.taobao.com要点诠释:(1)在判断充分条件与必要条件时,首先要分清哪是条件,哪是结论...