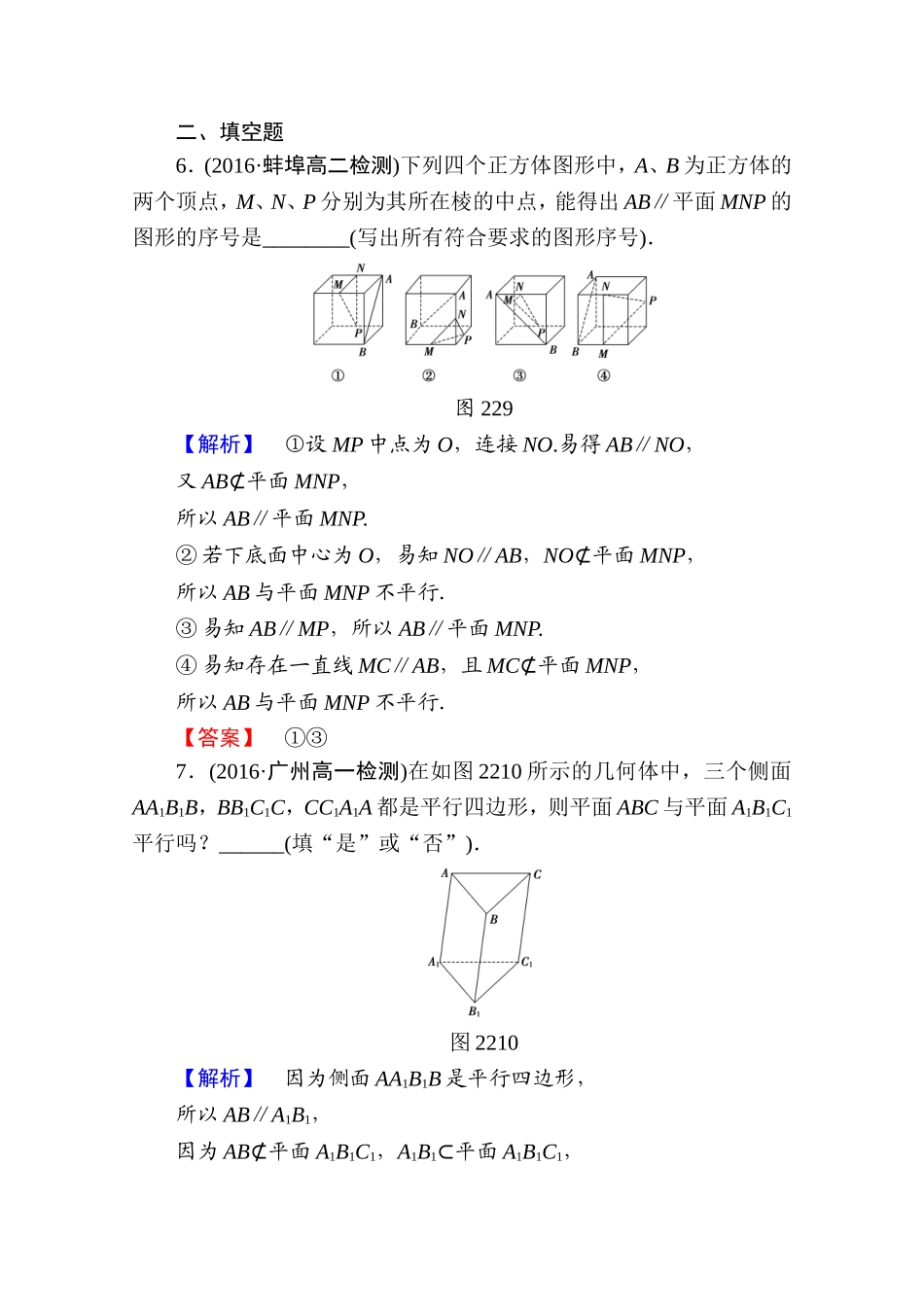
学业分层测评(十)(建议用时:45分钟)[达标必做]一、选择题1.若直线l不平行于平面α,且l⊄α,则()A.α内的所有直线与l异面B.α内不存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交【解析】直线l不平行于平面α,且l⊄α,所以l与α相交,故选B.【答案】B2.已知m,n是两条直线,α,β是两个平面.有以下说法:①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;②若m∥α,m∥β,则α∥β;③若m∥α,n∥β,m∥n,则α∥β.其中正确的个数是()A.0B.1C.2D.3【解析】把符号语言转换为文字语言或图形语言.可知①是面面平行的判定定理;②③中平面α、β还有可能相交,所以选B.【答案】B3.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为()A.平行B.相交C.平行或相交D.可能重合【解析】若三点分布于平面β的同侧,则α与β平行,若三点分布于平面β的两侧,则α与β相交.【答案】C4.如果AB、BC、CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是()【导学号:09960062】A.平行B.相交C.AC在此平面内D.平行或相交【解析】把这三条线段放在正方体内如图,显然AC∥EF,AC⊄平面EFG.EF⊂平面EFG,故AC∥平面EFG.故选A.【答案】A5.如图228,P为平行四边形ABCD所在平面外一点,Q为PA的中点,O为AC与BD的交点,下面说法错误的是()图228A.OQ∥平面PCDB.PC∥平面BDQC.AQ∥平面PCDD.CD∥平面PAB【解析】因为O为▱ABCD对角线的交点,所以AO=OC,又Q为PA的中点,所以QO∥PC.由线面平行的判定定理,可知A、B正确,又ABCD为平行四边形,所以AB∥CD,故CD∥平面PAB,故D正确.【答案】C二、填空题6.(2016·蚌埠高二检测)下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是________(写出所有符合要求的图形序号).图229【解析】①设MP中点为O,连接NO.易得AB∥NO,又AB⊄平面MNP,所以AB∥平面MNP.②若下底面中心为O,易知NO∥AB,NO⊄平面MNP,所以AB与平面MNP不平行.③易知AB∥MP,所以AB∥平面MNP.④易知存在一直线MC∥AB,且MC⊄平面MNP,所以AB与平面MNP不平行.【答案】①③7.(2016·广州高一检测)在如图2210所示的几何体中,三个侧面AA1B1B,BB1C1C,CC1A1A都是平行四边形,则平面ABC与平面A1B1C1平行吗?______(填“是”或“否”).图2210【解析】因为侧面AA1B1B是平行...