高中数学人教A版选修2-1 第二章 圆锥曲线与方程 2.1.1、2.1.2 Word版含答案.doc

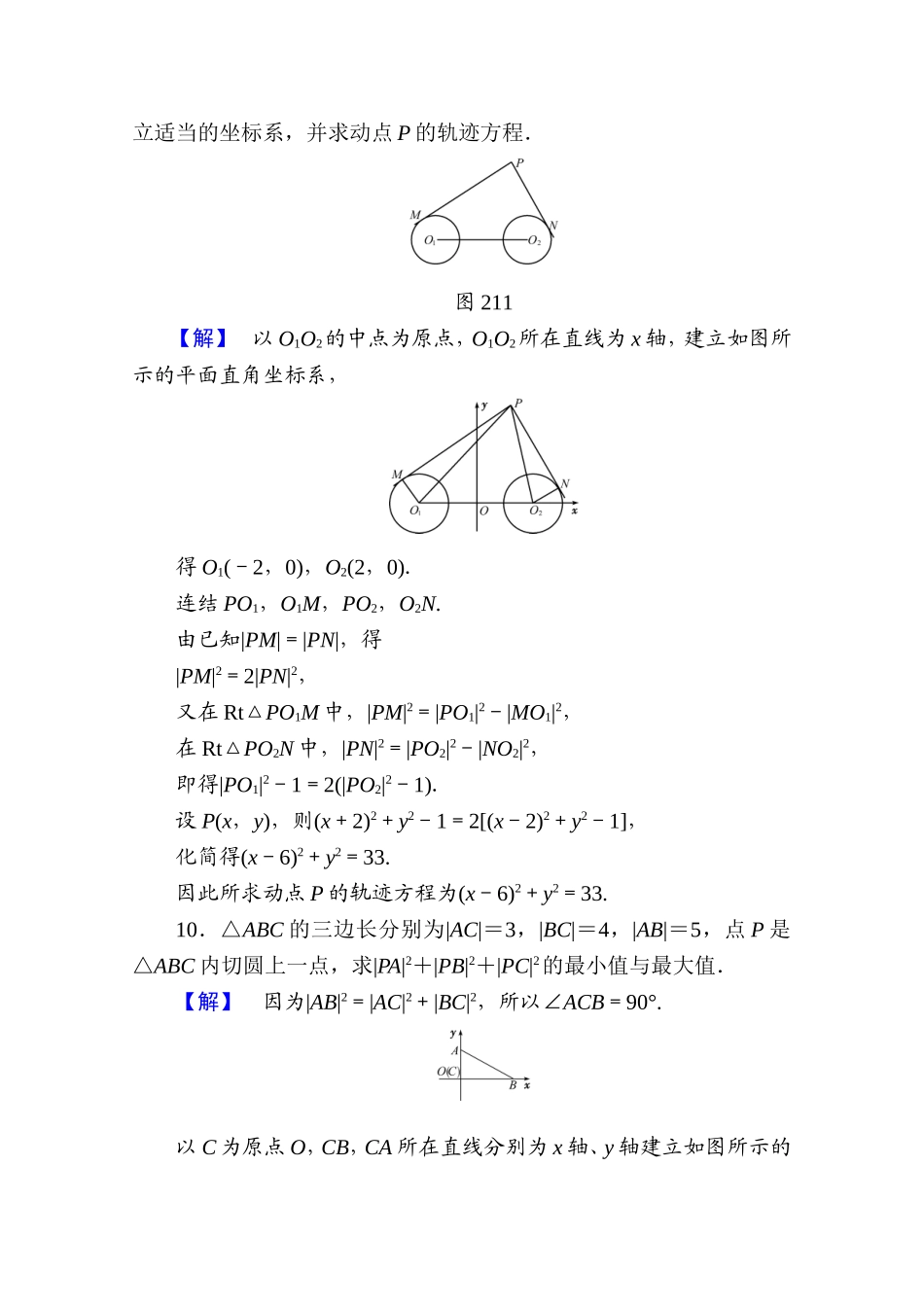
学业分层测评 (建议用时：45分钟) [学业达标] 一、选择题 1．曲线x2－xy－y2－3x＋4y－4＝0与x轴的交点坐标是(　　) A．(4，0)和(－1，0)　　 B．(4，0)和(－2，0) C．(4，0)和(1，0) D．(4，0)和(2，0) 【解析】　在曲线x2－xy－y2－3x＋4y－4＝0中，令y＝0，则x2－3x－4＝0，∴x＝－1或x＝4. ∴交点坐标为(－1，0)和(4，0)． 【答案】　A 2．方程(x2－4)(y2－4)＝0表示的图形是(　　) A．两条直线 B．四条直线 C．两个点 D．四个点 【解析】　由(x2－4)(y2－4)＝0得(x＋2)(x－2)(y＋2)·(y－2)＝0，所以x＋2＝0或x－2＝0或y＋2＝0或y－2＝0，表示四条直线． 【答案】　B 3．在平面直角坐标系xOy中，若定点A(1，2)与动点P(x，y)满足·＝4，则点P的轨迹方程是(　　) A．x＋y＝4 B．2x＋y＝4 C．x＋2y＝4 D．x＋2y＝1 【解析】　由＝(x，y)，＝(1，2)得·＝(x，y)·(1，2)＝x＋2y＝4，则x＋2y＝4即为所求的轨迹方程，故选C. 【答案】　C 4．方程(2x－y＋2)·＝0表示的曲线是(　　) A．一个点与一条直线 B．两个点 C．两条射线或一个圆 D．两个点或一条直线或一个圆 【解析】　原方程等价于x2＋y2－1＝0，即x2＋y2＝1，或故选C. 【答案】　C 5．已知方程y＝a|x|和y＝x＋a(a＞0)所确定的两条曲线有两个交点，则a的取值范围是(　　) A．a＞1 B．0＜a＜1 C．0＜a＜1或a＞1 D．a∈∅ 【答案】　A 二、填空题 6．“曲线C上的点的坐标都是方程f(x，y)＝0的解”是“方程f(x，y)＝0是曲线C的方程”的________条件． 【解析】　“方程f(x，y)＝0是曲线C的方程 ”⇒“曲线C上的点的坐标都是方程f(x，y)＝0的解”，反之不成立． 【答案】　必要不充分 7．方程·(x＋y＋1)＝0表示的几何图形是________________． 【解析】　由方程得或x－3＝0， 即x＋y＋1＝0(x≥3)或x＝3. 【答案】　一条射线和一条直线 8．(2016·广东省华南师大附中月考)已知定点F(1，0)，动点P在y轴上运动，点M在x轴上，且·＝0，延长MP到点N，使得||＝||，则点N的轨迹方程是________. 【导学号：18490037】 【解析】　由于||＝||，则P为MN的中点．设N(x，y)，则M(－x，0)，P，由·＝0，得·＝0，所以(－x)·1＋·＝0，则y2＝4x，即点N的轨迹方程是y2＝4x. 【答案】　y2＝4x 三、解答题 9．如图2­1­1，圆O1与圆O2的半径都是1，|O1O2|＝4，过动点P分别作圆O1、圆O2的切线PM，PN(M，N分别为切点)，使得|PM|＝|PN|，试建立适当的坐标系，并求动点P的轨迹方程． 图2­1­1 【解】　以O1O2的中点为原点，O1O2所在直线为x轴，建立如图所示的平面直角坐标系， 得O1(－2，0)，O2(2，0)． 连结PO1，O1M，PO2，O2N. 由已知|PM|＝|PN|，得 |PM|2＝2|PN|2， 又在Rt△PO1M中，|PM|2＝|PO1|2－|MO1|2， 在Rt△PO2N中，|PN|2＝|PO2|2－|NO2|2， 即得|PO1|2－1＝2(|PO2|2－1)． 设P(x，y)，则(x＋2)2＋y2－1＝2[(x－2)2＋y2－1]， 化简得(x－6)2＋y2＝33. 因此所求动点P的轨迹方程为(x－6)2＋y2＝33. 10．△ABC的三边长分别为|AC|＝3，|BC|＝4，|AB|＝5，点P是△ABC内切圆上一点，求|PA|2＋|PB|2＋|PC|2的最小值与最大值． 【解】　因为|AB|2＝|AC|2＋|BC|2，所以∠ACB＝90°. 以C为原点O，CB，CA所在直线分别为x轴、y轴建立如图所示的平面直角坐标系，由于|AC|＝3，|BC|＝4，得C(0，0)，A(0，3)，B(4，0)． 设△ABC内切圆的圆心为(r，r)， 由△ABC的面积＝×3×4＝r＋2r＋r， 得r＝1， 于是内切圆的方程为(x－1)2＋(y－1)2＝1⇒x2＋y2＝2x＋2y－1， 由(x－1)2≤1⇒0≤x≤2. 设P(x，y)，那么|PA|2＋|PB|2＋|PC|2＝x2＋(y－3)2＋(x－4)2＋y2＋x2＋y2＝3(x2＋y2)－8x－6y＋25＝3(2x＋2y－1)－8x－6y＋25＝22－2x， 所以当x＝0时，|PA|2＋|PB|2＋|PC|2取最大值为22， 当x＝2时取最小值为18. [能力提升] 1．到点A(0，0)，B(－3，4)的距离之和为5的轨迹方程是(　　) A．y＝－x(－3≤x≤0) B．y＝－x(0≤x≤4) C．y＝－x(－3≤x≤4) D．y＝－x(0≤x≤5) 【解析】　注意到|AB|＝5，则满足到点A(0，0)，B(－3，4)的距离之和为5的点必在线段AB上，因此，方程为y＝－x(－3≤x≤0)，故选A. 【答案】　A 2．(2016·河南省实验中学月考)已知动点P到定点(1，0)和定直线x＝3的距离之和为4，则点P的轨迹方程为(　　) A．y2＝4x B．y2＝－12(x－4) C．y2＝4x(x≥3)或y2＝－12(x－4)(x<3) D．y2＝4x(x≤3)或y2＝－12(x－4)(x>3) 【解析】　设P(x，y)，由题意得＋|x－3|＝4.若x≤3，则y2＝4x；若x>3，则y2＝－12(x－4)，故选D. 【答案】　D 3．已知两定点A(－2，0)，B(1，0)，如果动点P满足|PA|＝2|PB|，则点P的轨迹所包围的图形的面积等于________． 【解析】　设动点P(x，y)， 依题意|PA|＝2|PB|， ∴＝2， 化简得(x－2)2＋y2＝4， 方程表示半径为2的圆， 因此图形的面积S＝π·22＝4π. 【答案】　4π 4．过点P(2，4)作两条互相垂直的直线l1、l2，若l1交x轴于A点，l2交y轴于B点，求线段AB的中点M的轨迹方程. 【导学号：18490038】 【解】　法一　设点M的坐标为(x，y)， ∵M为线段AB的中点， ∴A点的坐标为(2x，0)，B点的坐标为(0，2y)． ∵l1⊥l2，且l1，l2过点P(2，4)， ∴PA⊥PB，即kPA·kPB＝－1， 而kPA＝＝(x≠1)， kPB＝＝， ∴·＝－1(x≠1)， 整理得x＋2y－5＝0(x≠1)． ∵当x＝1时，A，B的坐标分别为(2，0)，(0，4)， ∴线段AB的中点坐标是(1，2)，它满足方程x＋2y－5＝0. 综上所述，点M的轨迹方程是x＋2y－5＝0. 法二　设点M的坐标为(x，y)，则A，B两点的坐标分别是(2x，0)，(0，2y)，连结PM. ∵l1⊥l2，∴2|PM|＝|AB|. 而|PM|＝， |AB|＝， ∴2＝， 化简得x＋2y－5＝0，即为所求的点M的轨迹方程.