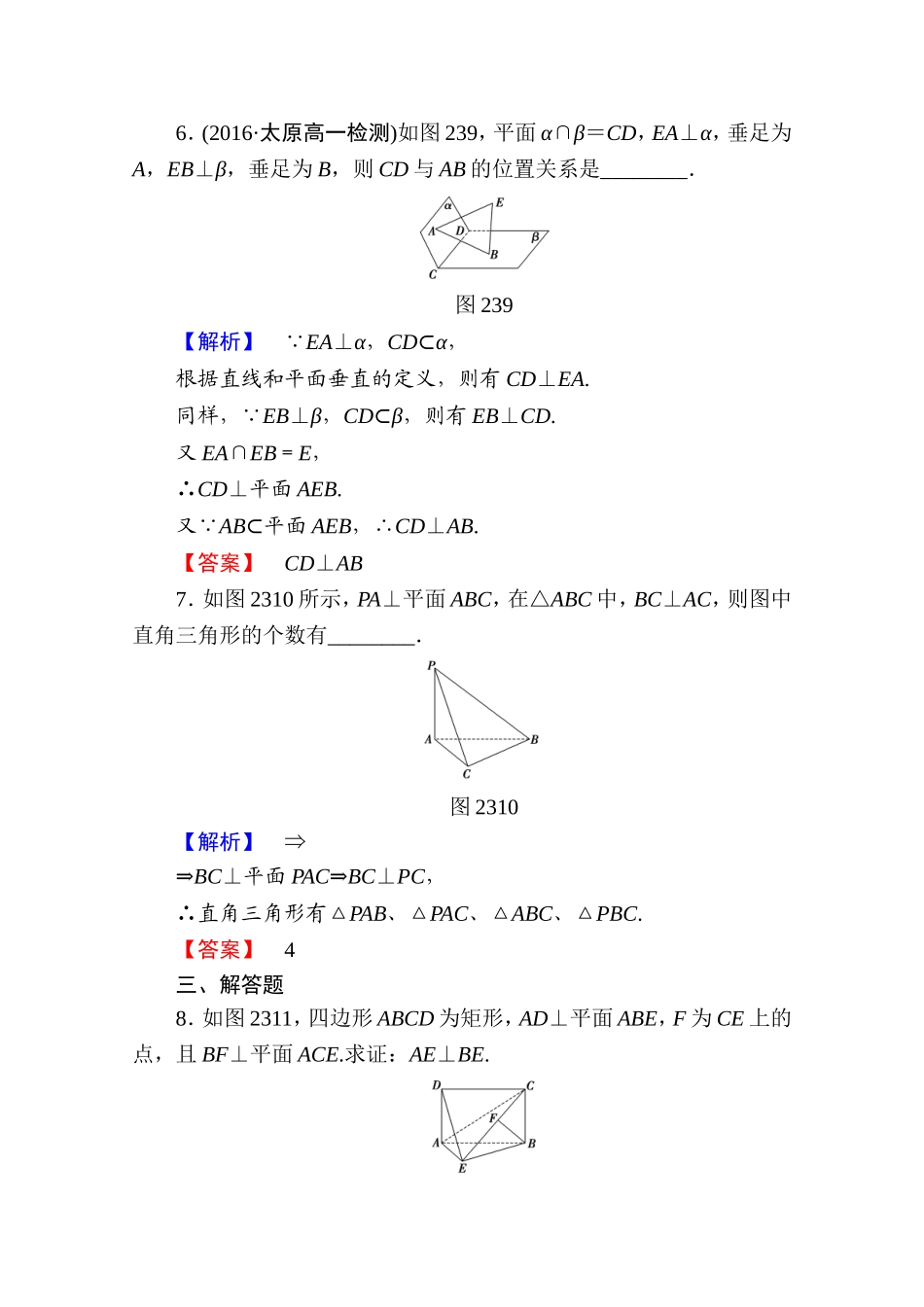
学业分层测评(十二)(建议用时:45分钟)[达标必做]一、选择题1.下列条件中,能使直线m⊥平面α的是()A.m⊥b,m⊥c,b⊥α,c⊥αB.m⊥b,b∥αC.m∩b=A,b⊥αD.m∥b,b⊥α【解析】由线线平行及线面垂直的判定知选项D正确.【答案】D2.如图238,三棱锥PABC中,PA⊥AB,PA⊥BC,则直线PB和平面ABC所成的角是()图238A.∠BPAB.∠PBAC.∠PBCD.以上都不对【解析】由PA⊥AB,PA⊥BC,AB∩BC=B,得PA⊥平面ABC,所以∠PBA为BP与平面ABC所成的角.故选B.【答案】B3.已知直线m,n是异面直线,则过直线n且与直线m垂直的平面()【导学号:09960073】A.有且只有一个B.至多一个C.有一个或无数个D.不存在【解析】若异面直线m、n垂直,则符合要求的平面有一个,否则不存在.【答案】B4.在正方体ABCDA1B1C1D1中,BB1与平面ACD1所成角的余弦值为()A.B.C.D.【解析】如图所示,连接BD交AC于点O,连接D1O,由于BB1∥DD1,∴DD1与平面ACD1所成的角就是BB1与平面ACD1所成的角.易知∠DD1O即为所求.设正方体的棱长为1,则DD1=1,DO=,D1O=,∴cos∠DD1O===.∴BB1与平面ACD1所成的角的余弦值为.【答案】D5.(2015·成都高二检测)已知ABCDA1B1C1D1为正方体,下列结论错误的是()A.BD∥平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1D.AC1⊥BD1【解析】正方体中由BD∥B1D1,易知A正确;由BD⊥AC,BD⊥CC1可得BD⊥平面ACC1,从而BD⊥AC1,即B正确;由以上可得AC1⊥B1D1,同理AC1⊥D1C,因此AC1⊥平面CB1D1,即C正确;由于四边形ABC1D1不是菱形,所以AC1⊥BD1不正确.故选D.【答案】D二、填空题6.(2016·太原高一检测)如图239,平面α∩β=CD,EA⊥α,垂足为A,EB⊥β,垂足为B,则CD与AB的位置关系是________.图239【解析】 EA⊥α,CD⊂α,根据直线和平面垂直的定义,则有CD⊥EA.同样, EB⊥β,CD⊂β,则有EB⊥CD.又EA∩EB=E,∴CD⊥平面AEB.又 AB⊂平面AEB,∴CD⊥AB.【答案】CD⊥AB7.如图2310所示,PA⊥平面ABC,在△ABC中,BC⊥AC,则图中直角三角形的个数有________.图2310【解析】⇒⇒BC⊥平面PAC⇒BC⊥PC,∴直角三角形有△PAB、△PAC、△ABC、△PBC.【答案】4三、解答题8.如图2311,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE.求证:AE⊥BE.图2311【证明】 AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE.又AE⊂平面ABE,∴AE⊥BC. BF⊥平面ACE,AE⊂平面ACE,∴AE⊥BF.又 BF⊂平面BCE,BC⊂平面BCE,BF∩BC=B,∴AE⊥平面B...