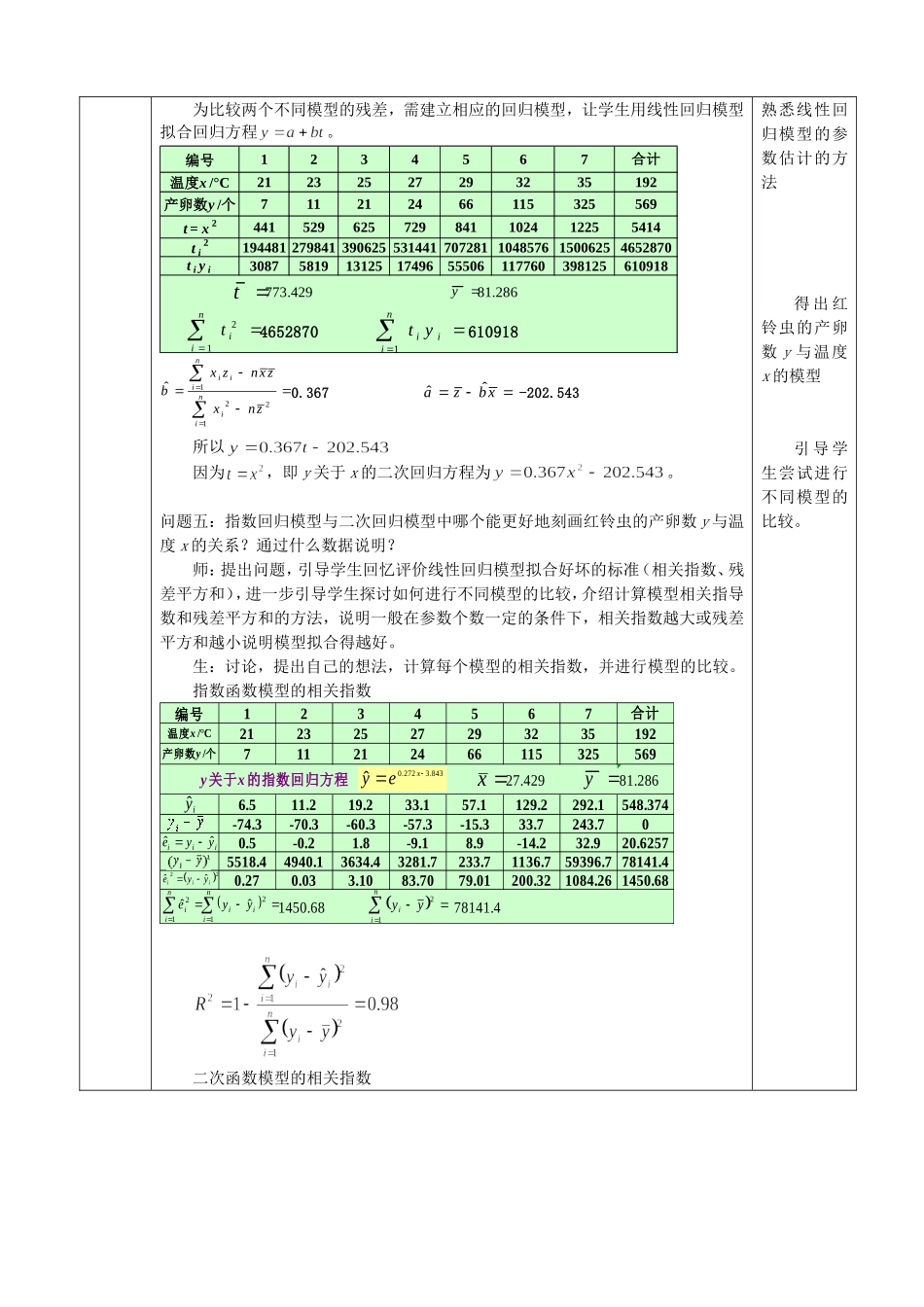
§3.1回归分析的基本思想及其初步(3)【学情分析】:教学对象是高二理科学生,学生已经学会建立回归模型的基本步骤,并有检验回归方程的拟合精确度的方法,并能解决一些实际问题。两个变量不呈线性关系,不能直接利用线性回归方程建立两个变量的关系,通过探究使学生体会对回归模型的选择,非线性模型可以通过变换转化为线性回归模型,让学生直观的观察、思考,借助于线性回归模型研究呈非线性关系的两个变量之间的关系,并通过回归分析体会不同模型拟合数据的效果。【教学目标】:(1)知识与技能:了解回归模型的选择;进一步理解非线性模型通过变换转化为线性回归模型;体会不同模型拟合数据的效果。(2)过程与方法:从实例出发,求出相应的回归直线方程,从中也找出存在的不足,从而有进行回归分析的必要性,通过学习相关指数,用相关指数来刻画回归的效果,进而归纳出回归分析的一般步骤,并对具体问题进行回归分析,用于解决实际问题。(3)情感态度与价值观:任何事物都是相对的,但又有一定的规律性,我们只要从实际出发,不断探求事物的内在联系,就会找出其中的规律性,形成解决实际问题的方法和能力。【教学重点】:1.加深体会有些非线性模型通过变换可以转化为线性回归模型;2.了解在解决问题的过程中寻找更好的模型的方法。【教学难点】:1.了解常用函数的图像特点,选择不同的模型建模;2.通过比较相关指数对不同的模型进行比较。【教学过程设计】:教学环节教学活动设计意图一、复习引入问题一:你能回忆一下建立回归模型的基本步骤?师:提出问题,引导学生回忆建立回归模型的基本步骤(选变量、画散点图、选模型、估计参数、分析与预测)生:回忆、叙述建立回归模型的基本步骤复习建立线性回归模型的基本步骤二、探究新知问题二:观察例2的图1.1-6中的散点图,红铃虫的产卵数y与温度x的图像特点:随着自变量的增加,因变量也随之增加。这些点可以除了可以看作是落在指数函数模型上,还可以认为它是落在什么函数的模型上?师:引导学生观察散点图的特点,并引导学生探究红铃虫的产卵数y与温度x还可能是什么关系。(二次函数模型)生:讨论、回忆一些常见函数图像的特点,判断红铃虫的产卵数y与温度x的可能关系样本点还可以看作是分布在二次函数曲线的周围。引导学生根据散点图判断两个变量的关系,使学生了解不是任何两个变量都一定是只有一种关系。产卵数与温度的关系050100150200250300350202224262830323436温度产卵数y/个问...