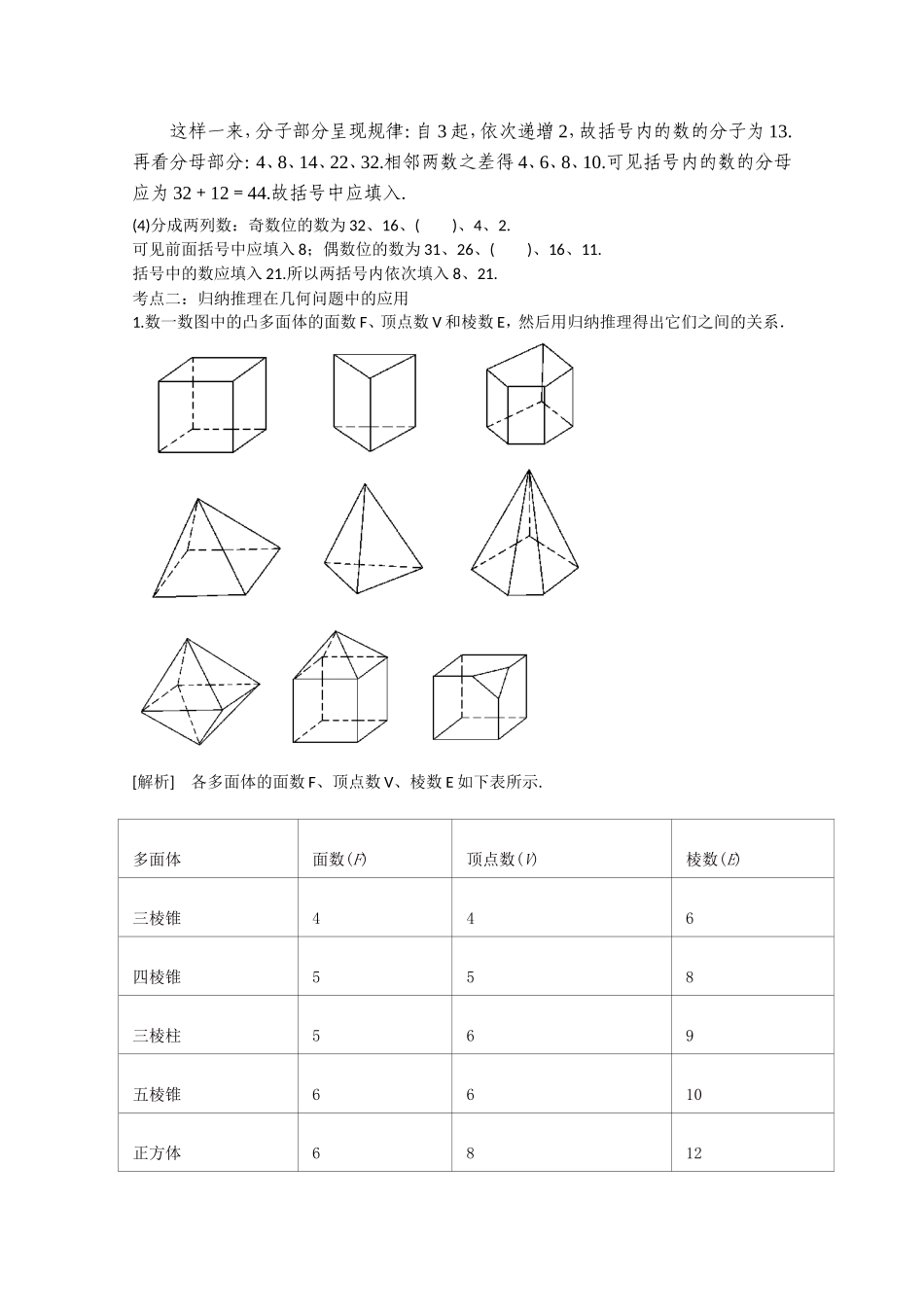
2.1..1合情推理考点一:归纳推理在数列中的应用1.根据下列条件,写出数列中的前4项,并归纳猜想它的通项公式.(1)a1=3,an+1=2an+1;(2)a1=a,an+1=;(3)对一切的n∈N*,an>0,且2=an+1.[解析](1)由已知有a1=3=22-1,a2=2a1+1=2×3+1=7=23-1,[来源:学优高考网]a3=2a2+1=2×7+1=15=24-1,[来源:学优高考网gkstk]a4=2a3+1=2×15+1=31=25-1.猜测出an=2n+1-1,n∈N*(n≥2).(2)由已知有a1=a,a2==,a3==,[来源:学优高考网gkstk]a4==.猜测出an=.(n≥2)2.下面各列数都依照一定规律排列,在括号里填上适当的数:(1)1、5、9、13、17、();(2)、1、1、2、3、();(3)、、、、、();(4)32、31、16、26、()、()、4、16、2、11.[答案](1)21(2)5(3)(4)821[解析]要在括号里填上适当的数,必须正确地判断出每列数所具有的规律,为此必须进行仔细的观察和揣摩.(1)考察相邻两数的差:5-1=4,9-5=4,13-9=4,17-13=4可见,相邻两数之差都是4.按此规律,括号里的数减去17等于4,所以括号里的数是17+4=21.(2)像(1)那样考虑难以发现规律,改变一下角度,把各数改写为、1、、、.可以发现:1÷=,÷1=,÷=,÷=.后一个数是前一个数的倍,按照这个规律,括号中的数应是×==5.(3)为探究规律,作适当变形:[来源:学优高考网]、、、、.这样一来,分子部分呈现规律:自3起,依次递增2,故括号内的数的分子为13.再看分母部分:4、8、14、22、32.相邻两数之差得4、6、8、10.可见括号内的数的分母应为32+12=44.故括号中应填入.(4)分成两列数:奇数位的数为32、16、()、4、2.可见前面括号中应填入8;偶数位的数为31、26、()、16、11.括号中的数应填入21.所以两括号内依次填入8、21.考点二:归纳推理在几何问题中的应用1.数一数图中的凸多面体的面数F、顶点数V和棱数E,然后用归纳推理得出它们之间的关系.[解析]各多面体的面数F、顶点数V、棱数E如下表所示.多面体面数(F)顶点数(V)棱数(E)三棱锥446四棱锥558[来源:学优高考网gkstk]三棱柱569五棱锥6610正方体6812正八面体8612五棱柱71015截角正方体71015尖顶塔9916观察其数字特征:4+4-6=2;5+5-8=2;5+6-9=2;6+6-10=2;6+8-12=2;8+6-12=2;7+10-15=2;9+9-16=2.可以发现,它们的顶点数V,棱数E及面数F有共同的关系式:V+F-E=2.2.平面内有n条直线,其中任何两条都不平行,任何三条不过同一点,试归纳它们的交点个数.[解析]n=2时,交点...