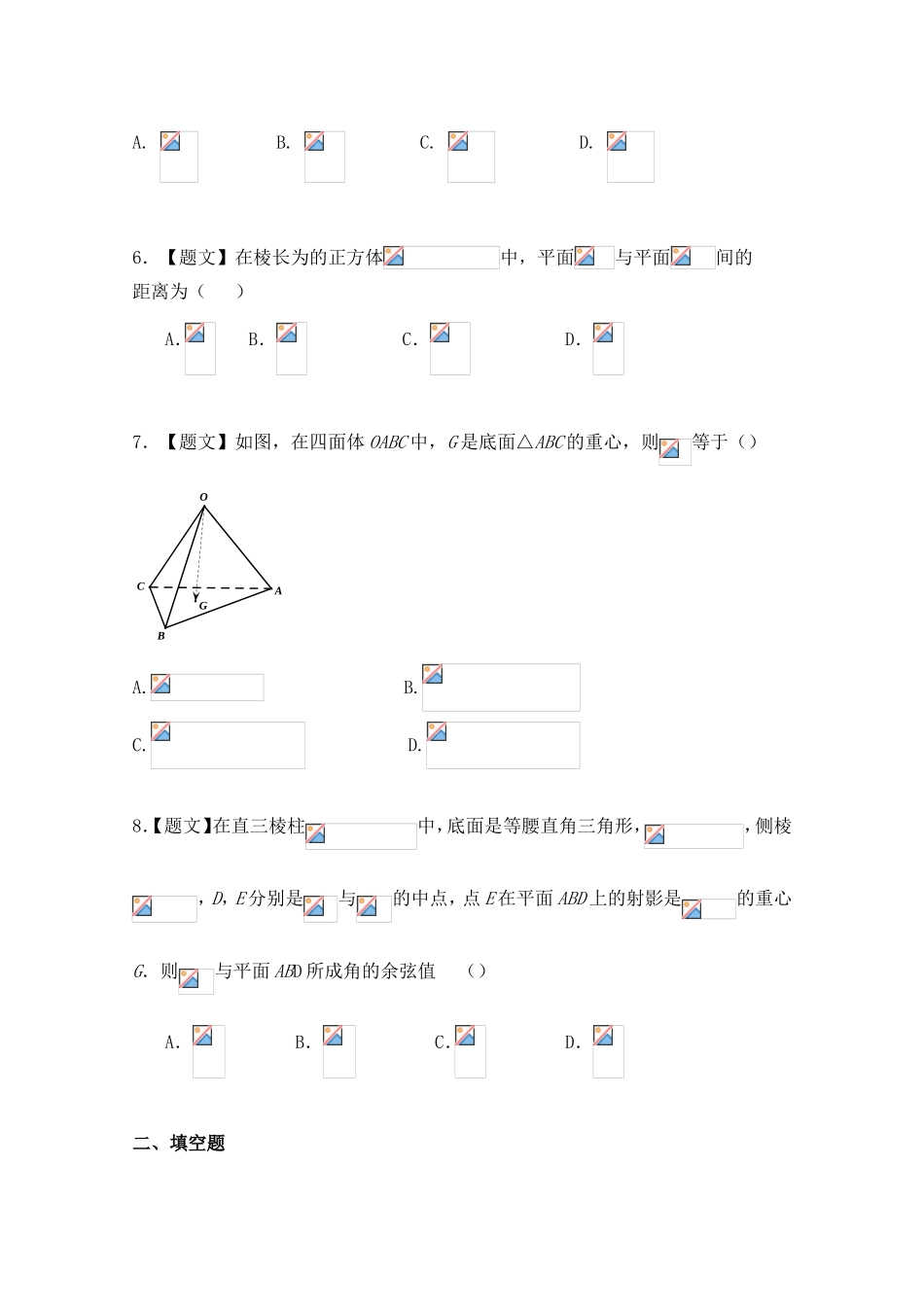
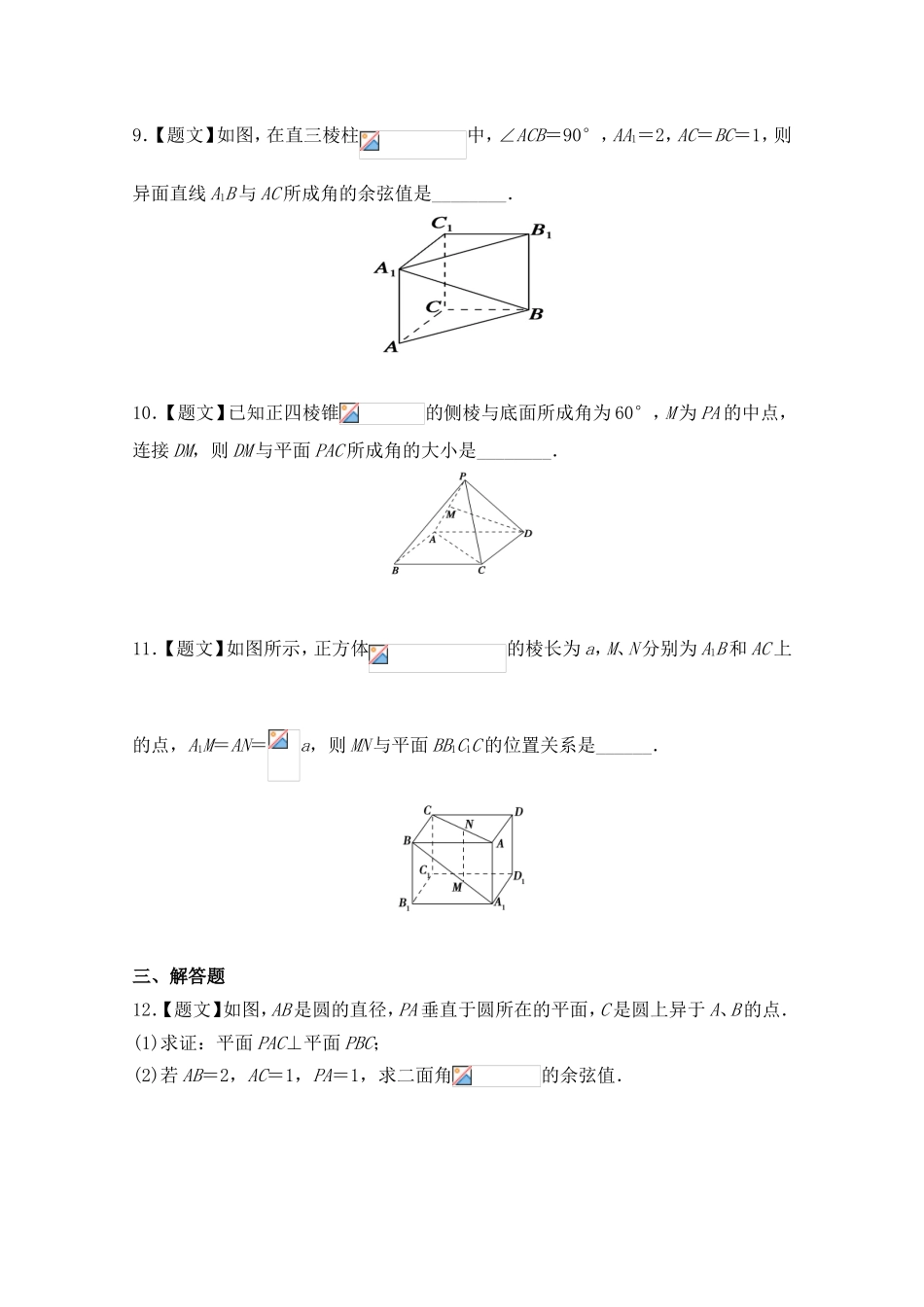
绝密★启用前人教版选修2-1课时3.2立体几何中的向量方法一、选择题1.【题文】已知三条直线l1,l2,l3的一个方向向量分别为a=(4,-1,0),b=(1,4,5),c=(-3,12,-9),则()A.l1⊥l2,但l1与l3不垂直B.l1⊥l3,但l1与l2不垂直C.l2⊥l3,但l2与l1不垂直D.l1,l2,l3两两互相垂直2.【题文】已知直线l1的方向向量为a=(2,4,x),直线l2的方向向量为b=(2,y,2),若|a|=6,且a⊥b,则x+y的值是()A.-3或1B.3或-1C.-3D.13.【题文】已知,,,分别是平面,的法向量,则平面,的位置关系式()A.平行B.垂直C.所成的二面角为锐角D.所成的二面角为钝角4.【题文】在空间直角坐标系中,点是在坐标平面内的射影,为坐标原点,则等于()A.B.C.D.5.【题文】长方体中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为()A.B.C.D.6.【题文】在棱长为的正方体中,平面与平面间的距离为()A.B.C.D.7.【题文】如图,在四面体OABC中,G是底面△ABC的重心,则等于()GCABOA.B.C.D.8.【题文】在直三棱柱中,底面是等腰直角三角形,,侧棱,D,E分别是与的中点,点E在平面ABD上的射影是的重心G.则与平面ABD所成角的余弦值()A.B.C.D.二、填空题9.【题文】如图,在直三棱柱中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是________.10.【题文】已知正四棱锥的侧棱与底面所成角为60°,M为PA的中点,连接DM,则DM与平面PAC所成角的大小是________.11.【题文】如图所示,正方体的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=a,则MN与平面BB1C1C的位置关系是______.三、解答题12.【题文】如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上异于A、B的点.(1)求证:平面PAC⊥平面PBC;(2)若AB=2,AC=1,PA=1,求二面角的余弦值.13.【题文】如图,直三棱柱中,△ABC是等边三角形,D是BC的中点.(1)求证:A1B∥平面ADC1;(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.14.【题文】直四棱柱中,底面为菱形,且为延长线上的一点,面.设.(1)求二面角的大小;(2)在上是否存在一点,使面?若存在,求的值;若不存在说明理由.人教版选修2-1课时3.2立体几何中的向量方法参考答案与解析一、选择题1.【答案】A【解析】 a·b=(4,-1,0)·(1,4,5)=4-4+0=0,a·c=(4,-1,0)·(-3,12,-9)=-12-12+0=-24≠0.b·c=(1,4,5)·(-3,12,-9)=-3+48-45=0,∴a...