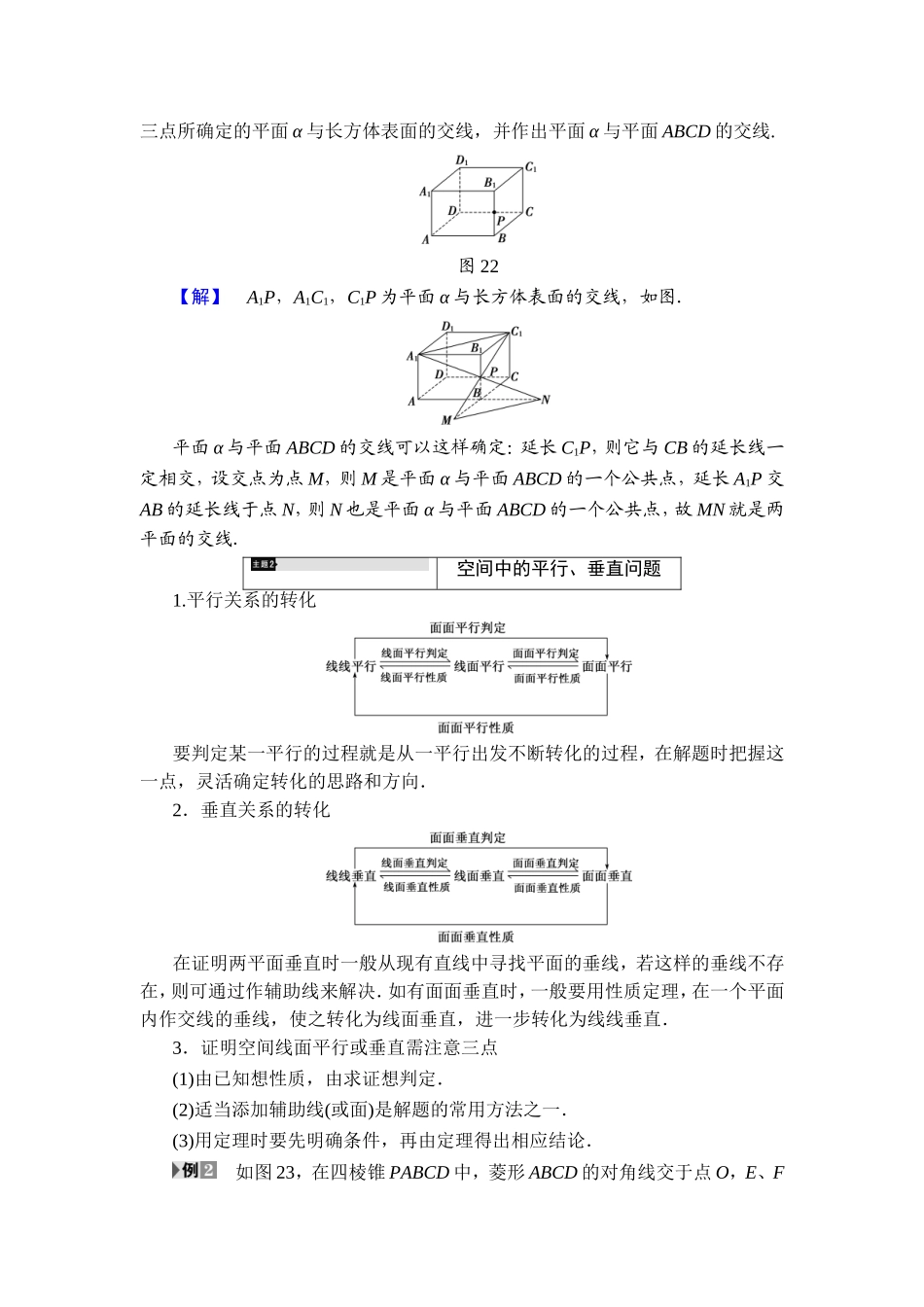
章末分层突破[自我校对]①确定平面的条件②异面直线③直线在平面内④直线与平面平行的判定定理⑤直线与平面平行的性质定理⑥平面与平面平行的判定定理⑦若α∥β,l⊂α,则l∥β⑧直线与平面垂直的判定定理⑨直线与平面垂直的定义⑩若l⊥α,l⊥β,则α∥β⑪平面与平面垂直的判定定理⑫平面与平面垂直的性质定理⑬直线与平面垂直的性质定理⑭二面角(教师用书独具)共点、共线、共面问题1.证明三线共点问题证明空间三线共点问题,先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上的问题.2.证明三点共线问题证明空间三点共线问题,通常证明这些点都在两个面的交线上,即先确定出某两点在某两个平面的交线上,再证明第三个点是两个平面的公共点,当然必在两个平面的交线上.3.证明共面问题证明共面问题,一般有两种证法:一是由某些元素确定一个平面,再证明其余元素在这个平面内;二是分别由不同元素确定若干个平面,再证明这些平面重合如图21所示,AB∩α=P,CD∩α=P,A,D与B,C分别在平面α的两侧,AC∩α=Q,BD∩α=R,求证:P,Q,R三点共线.图21【精彩点拨】要证若干点共线,需证这些点在两个相交平面内,且是这两个平面的公共点.【规范解答】 AB∩α=P,CD∩α=P,∴AB∩CD=P,∴AB,CD可确定一个平面,设为β. A∈AB,C∈CD,B∈AB,D∈CD,∴A∈β,C∈β,B∈β,D∈β.∴AC⊂β,BD⊂β,平面α,β相交. AB∩α=P,AC∩α=Q,BD∩α=R,∴P,Q,R三点是平面α与平面β的公共点.∴P,Q,R都在α与β的交线上.故P,Q,R三点共线.[再练一题]1.如图22,在长方体ABCDA1B1C1D1中,P为棱BB1的中点,画出由A1、C1、P三点所确定的平面α与长方体表面的交线,并作出平面α与平面ABCD的交线.图22【解】A1P,A1C1,C1P为平面α与长方体表面的交线,如图.平面α与平面ABCD的交线可以这样确定:延长C1P,则它与CB的延长线一定相交,设交点为点M,则M是平面α与平面ABCD的一个公共点,延长A1P交AB的延长线于点N,则N也是平面α与平面ABCD的一个公共点,故MN就是两平面的交线.空间中的平行、垂直问题1.平行关系的转化要判定某一平行的过程就是从一平行出发不断转化的过程,在解题时把握这一点,灵活确定转化的思路和方向.2.垂直关系的转化在证明两平面垂直时一般从现有直线中寻找平面的垂线,若这样的垂线不存在,则可通过作辅助线来解决.如有面面垂直时,一般要用性质定理,在一个平面内作...