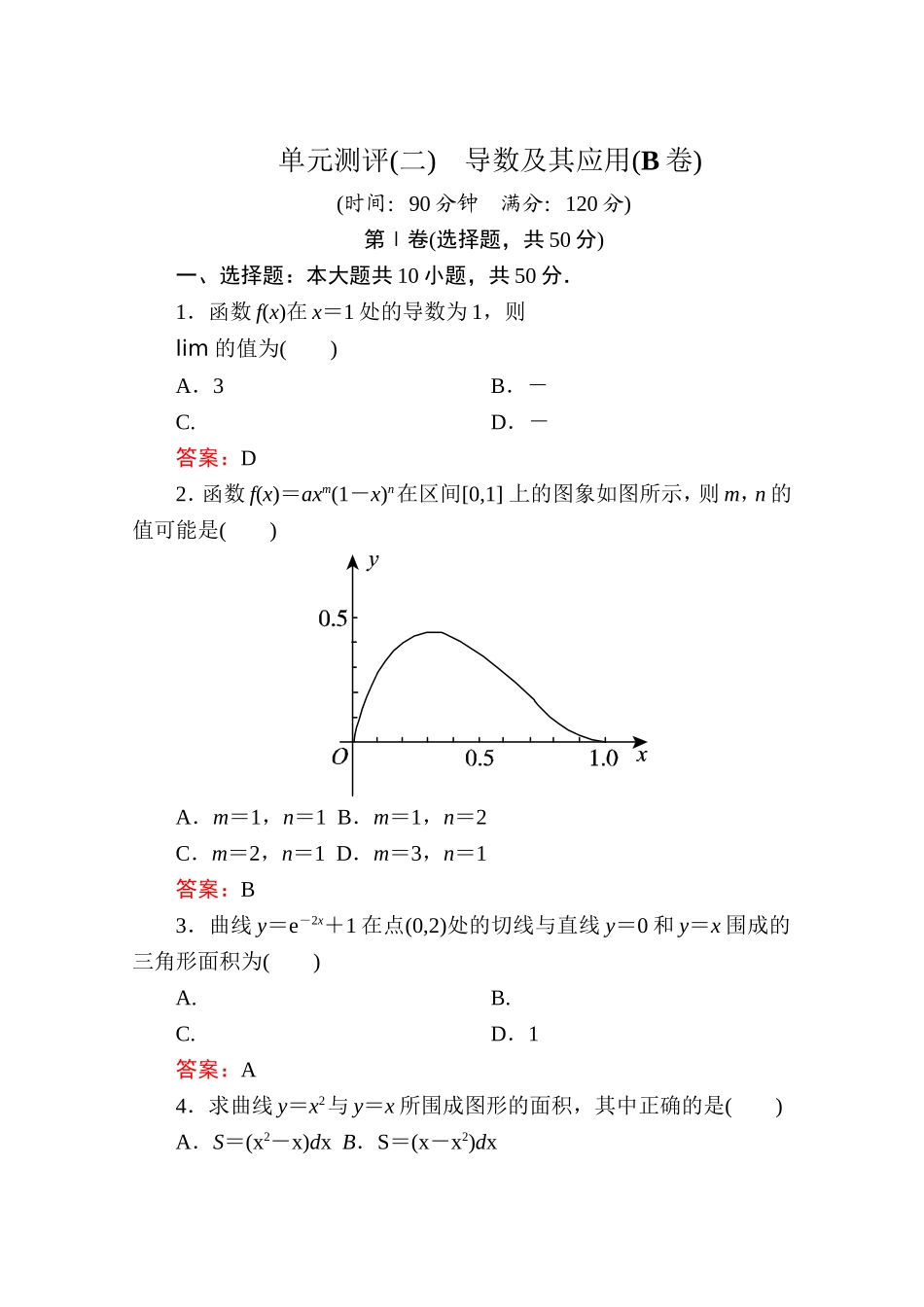
单元测评(二)导数及其应用(B卷)(时间:90分钟满分:120分)第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,共50分.1.函数f(x)在x=1处的导数为1,则lim的值为()A.3B.-C.D.-答案:D2.函数f(x)=axm(1-x)n在区间[0,1]上的图象如图所示,则m,n的值可能是()A.m=1,n=1B.m=1,n=2C.m=2,n=1D.m=3,n=1答案:B3.曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形面积为()A.B.C.D.1答案:A4.求曲线y=x2与y=x所围成图形的面积,其中正确的是()A.S=(x2-x)dxB.S=(x-x2)dxC.S=(y2-y)dxD.S=(y-)dy解析:两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x≥x2,故函数y=x2与y=x所围成图形的面积S=(x-x2)dx.答案:B5.已知实数a,b,c,d成等比数列,且函数y=ln(x+2)-x,当x=b时取到极大值c,则ad等于()A.-1B.0C.1D.2解析:y′=-1,令y′=0得x=-1,当-20,当x>-1时,y′<0,∴b=-1,c=ln(-1+2)-(-1)=1,∴ad=bc=-1,故选A.答案:A6.下列图象中,有一个是函数f(x)=x3+ax2+(a2-1)x+1(a∈R,a≠0)的导数f′(x)的图象,则f(-1)的值为()(1)(2)(3)A.B.-C.D.-或解析:f′(x)=x2+2ax+a2-1,其图象为开口向上的抛物线,故不是第一个图;第二个图中,a=0,f′(x)=x2-1,但已知a≠0,故f′(x)的图象为第三个图,∴f′(0)=0,∴a=±1,又其对称轴在y轴右边,∴a=-1,∴f(x)=x3-x2+1,∴f(-1)=-,故选B.答案:B7.已知曲线方程f(x)=sin2x+2ax(a∈R),若对任意实数m,直线l:x+y+m=0都不是曲线y=f(x)的切线,则a的取值范围是()A.(-∞,-1)∪(-1,0)B.(-∞,-1)∪(0,+∞)C.(-1,0)∪(0,+∞)D.a∈R且a≠0,a≠-1解析:若存在实数m,使直线l是曲线y=f(x)的切线, f′(x)=2sinxcosx+2a=sin2x+2a,∴方程sin2x+2a=-1有解,∴-1≤a≤0,故所求a的取值范围是(-∞,-1)∪(0,+∞),选B.答案:B8.设函数f(x)=ax2+b(a≠0),若f(x)dx=3f(x0),则x0=()A.±1B.C.±D.2解析:f(x)dx=(ax2+b)dx=|=9a+3b.由f(x)dx=3f(x0)得,9a+3b=3ax+3b,∴x=3,∴x0=±.答案:C9.设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)-f(x)g′(x)>0,且f(3)=0,则不等式f(x)g(x)<0的解集是()A.(-3,0)∪(3,+∞)B.(-3,0)∪(0,3)C.(-∞,-3)∪(3,+∞)D.(-∞...