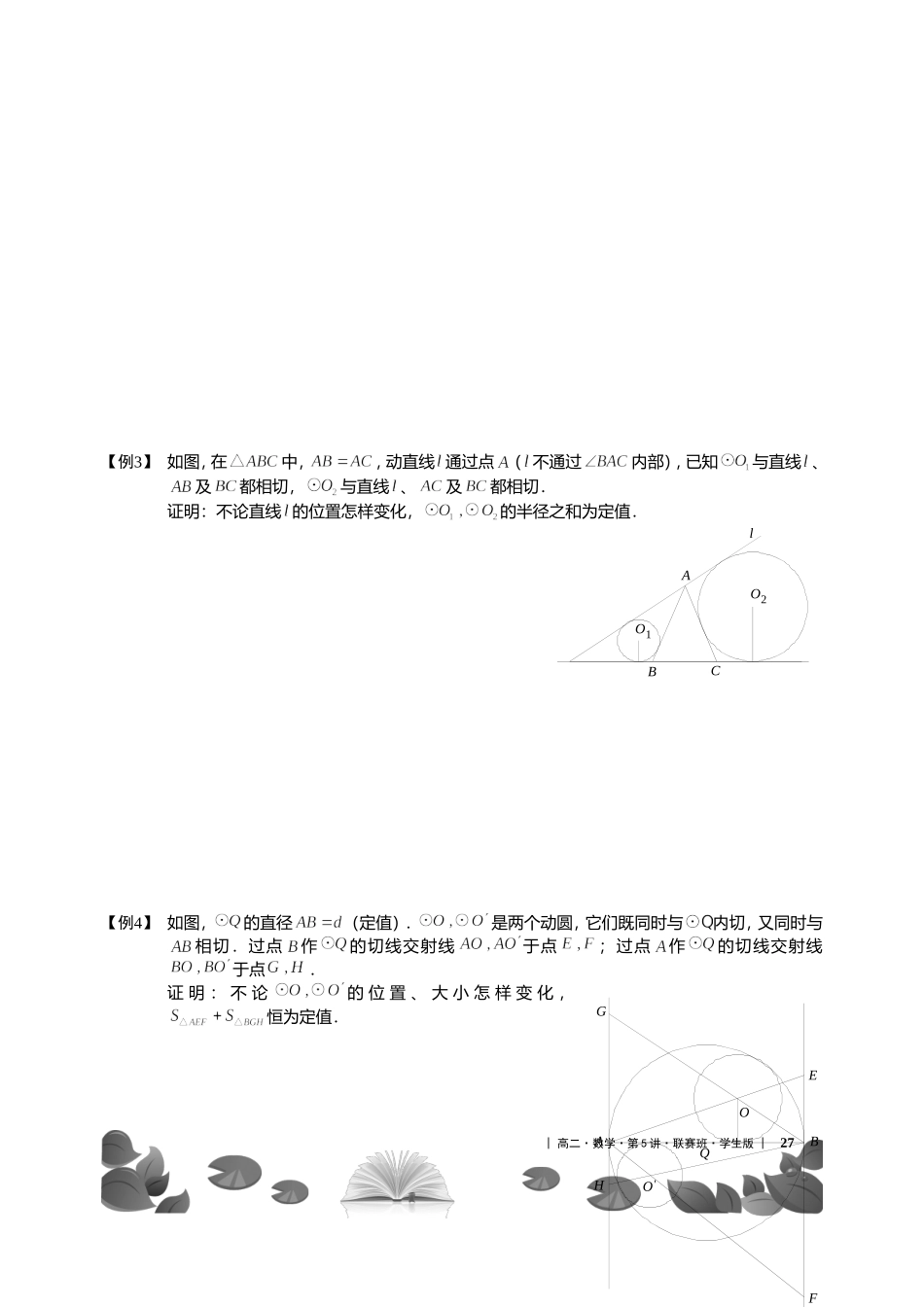
第五讲平面几何定值与最值名人名言罗素逻辑与数学之不同,就像孩子和大人一样;逻辑是数学的初期,而数学是逻辑的成年期.这是罗素就数学与逻辑的关系提出的一句名言.罗素(B.A.W.Russell,1872~1970,英国数理逻辑学家)是本世纪最有影响的哲学家之一,他的学术活动以哲学为主,涉及数学、物理学、历史、政治、教育、宗教等方面,并积极参加社会活动.1900年罗素接触到布尔和皮亚诺的符号逻辑,开始和怀特黑德合作,试图用逻辑推出全部数学.从1901年开始实行这项宏大的计划,经过10年的奋战写成了三大卷的《数学原理》.这部巨著对数理逻辑的发展做出了卓越的贡献,也使他赢得了崇高的声誉.在写这部书的过程中,罗素发现康托尔的集合论有矛盾,于是提出轰动一时的“罗素悖论”,几乎动摇了整个数学的基础.罗素还发展了类型论,引进等价类的概念,阐述数学哲学的思想,倡导数学基础的逻辑主义等,对20世纪数学的发展产生重大的影响.1950年作为“当代理性和人道的最杰出的代言人之一,西方自由言论和自由思想的无谓斗士”荣获诺贝尔文学奖.|高二·数学·第5讲·联赛班·学生版|25平面几何定值的求解思路:1.取特殊或极端位置猜测,在一般位置论证2.通过推导、计算平面几何最值的求解思路:1.图形中的特殊点2.注意到图形中元素间相互特殊关系3.引入变量,利用二次函数求极值4.引入三角函数,利用三角函数的极值性5.利用不等式6.运用有关结论:①周长一定的简单闭曲线的平面图形中,圆的面积最大;②面积一定的简单闭曲线的平面图形中,圆的周长最小;③周长一定的平面边形中,正边形面积最大;④面积一定的平面边形中,正边形周长最小.板块一平面几何定值【例1】如图,为正三角形,动点在直线上,过点作于.过点作的垂线交过所作的垂线于,交于.证明:恒为定值.【例2】如图,为半圆的直径,动点在半圆上,于点.与都相切,与都相切,切点在上.证明:不论点位置如何,恒为定值.知识点拨例题精讲26|高二·数学·第5讲·联赛班·学生版|O2O1OFEDCBAPFEDCBA【例3】如图,在中,,动直线通过点(不通过内部),已知与直线、及都相切,与直线、及都相切.证明:不论直线的位置怎样变化,的半径之和为定值.【例4】如图,的直径(定值).是两个动圆,它们既同时与内切,又同时与相切.过点作的切线交射线于点;过点作的切线交射线于点.证明:不论的位置、大小怎样变化,恒为定值.|高二·数学·第5讲·联赛班·学生版|27O2O1lCBAO'OQH...