北京课改初中数学九上《19.6相似三角形的性质》PPT课件 (1).pptVIP免费

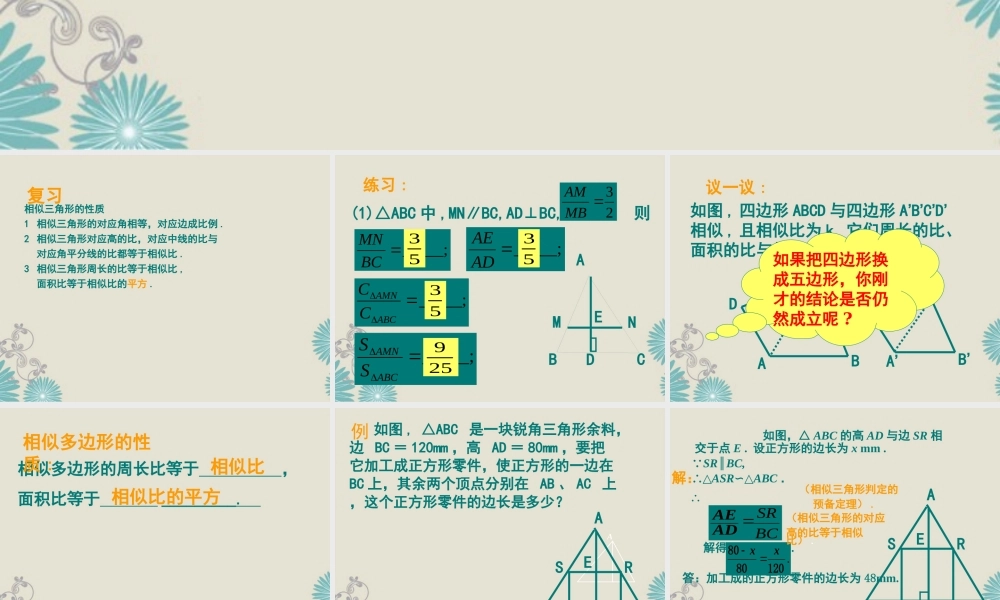
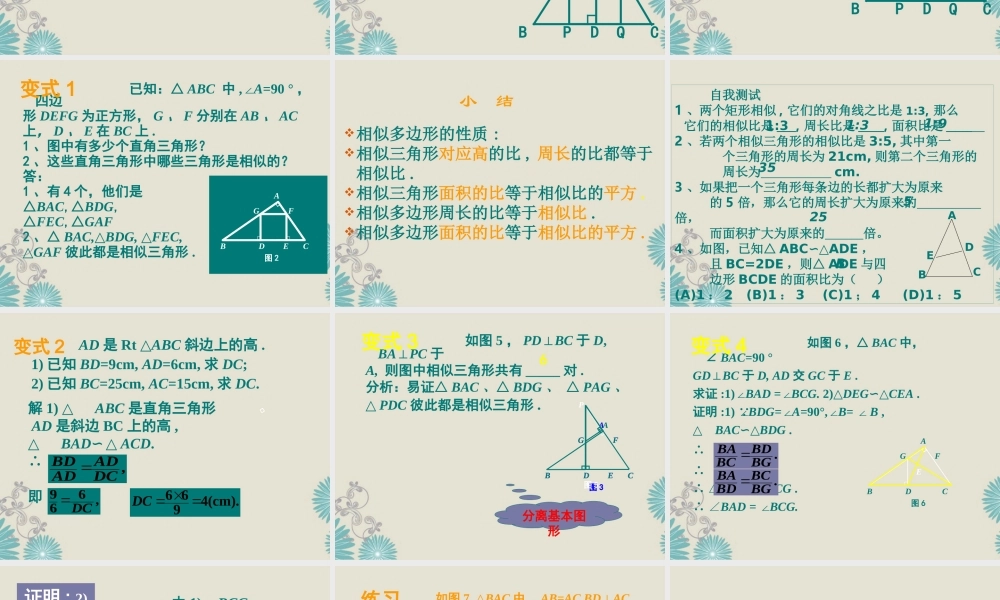
相似三角形的性质1相似三角形的对应角相等，对应边成比例.2相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比.3相似三角形周长的比等于相似比,面积比等于相似比的平方.复习练习:(1)△ABC中,MN∥BC,AD⊥BC,则23MBAM_____;BCMN_____;ADAE_____;ABCAMNCC_____;ABCAMNSSDABCMNE535353259议一议:如图,四边形ABCD与四边形A’B’C’D’相似,且相似比为k,它们周长的比、面积的比与相似比有什么关系?ABCDA’B’C’D’如果把四边形换成五边形，你刚才的结论是否仍然成立呢?相似多边形的周长比等于，面积比等于_________.相似比相似比的平方相似多边形的性质:如图,△ABC是一块锐角三角形余料，边BC＝120mm，高AD＝80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？例AABCSREPDQ如图，△ABC的高AD与边SR相交于点E.设正方形的边长为xmm. SR∥BC,∴△ASR∽△ABC．∴解得x=48(mm).答：加工成的正方形零件的边长为48mm.解：BCSRADAE．1208080xx（相似三角形的对应高的比等于相似比）.ABCSREPDQ（相似三角形判定的预备定理）.已知：△ABC中,∠A=90°，四边形DEFG为正方形，G、F分别在AB、AC上，D、E在BC上.1、图中有多少个直角三角形？2、这些直角三角形中哪些三角形是相似的？答：1、有4个，他们是△BAC,△BDG,△FEC,△GAF2、△BAC,△BDG,△FEC,△GAF彼此都是相似三角形.变式1BDECAGF图2小结相似多边形的性质:相似三角形对应高的比,周长的比都等于相似比.相似三角形面积的比等于相似比的平方.相似多边形周长的比等于相似比.相似多边形面积的比等于相似比的平方.自我测试1、两个矩形相似,它们的对角线之比是1:3,那么它们的相似比是___,周长比是____,面积比是____2、若两个相似三角形的相似比是3:5,其中第一个三角形的周长为21cm,则第二个三角形的周长为cm.3、如果把一个三角形每条边的长都扩大为原来的5倍，那么它的周长扩大为原来的倍，而面积扩大为原来的倍。4、如图，已知△ABC∽△ADE，且BC=2DE，则△ADE与四边形BCDE的面积比为（）(A)1：2(B)1：3(C)1；4(D)1：5ABCDE1:31:31:935525BAD是Rt△ABC斜边上的高.1)已知BD=9cm,AD=6cm,求DC;2)已知BC=25cm,AC=15cm,求DC.变式2解1)△△ABC是直角三角形AD是斜边BC上的高,△△BAD∽△ACD.∴即∴,DC669,DCADADBD4(cm).966DC如图5，PD⊥BC于D,BA⊥PC于A,则图中相似三角形共有_____对.分析：易...