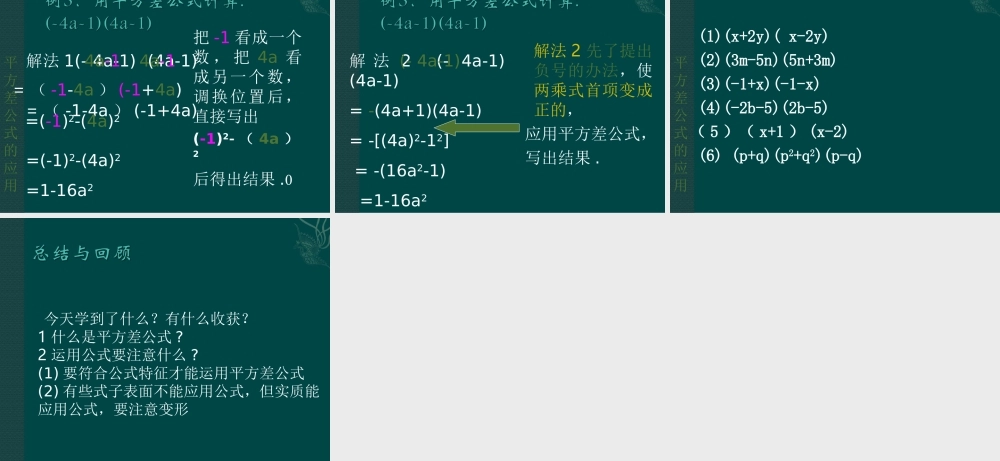
两个二项式相乘,在合并同类项前应该有几项?合并同类项以后,积可能会是三项吗?积可能是二项吗?请举出例子计算下面各题:(1)(a+5)(a-5)=__________;(2)(m+3)(m-3)=__________;(3)(3x+7)(3x-7)=__________;(4)(5a+b)(5a-b)=__________;(5)(n+3m)(n-3m)=__________,(6)(x+2y)(x-2y)=__________.通过计算你发现了什么规律?具有怎样特点的整式乘法,用你发现的规律去计算可以简化?(1)请你再举出例子并直接口算出结果。(2)请用文字语言把规律概括出来。(3)怎样证明这个规律的一般性呢?(当乘式是两个数之和以及这两个数之差相乘时,积是二项式这是因为具备这样特点的两个二项式相乘,积的四个项中,会出现互为相反数的两项,合并这两项的结果为零,于是就剩下两项了而它们的积等于乘式中这两个数的平方差)证明:∵(a+b)(a-b)=a2-ab+ab-b2(整式乘法)=a2-b2,∴(a+b)(a-b)=a2-b2(a+b)(a-b)=a2-b2平方差公式(a+b)(a-b)=a2-b2公式特征:公式的左边是两个数的和与这两个数的差积;公式的右边是这两个数的平方差。aabbba-b面积:(a+b)(a-b)=a2-b2例1用平方差公式计算:(1+5b)(1-5b)(a+b)(a-b)=a2-b2解:(1+5b)(1-5b)=12-(5b)2=1-25b2公式中的a和b可以表示数或代数式解:(1)(4y+3x)(3x-4y)=(3x)2-(4y)2=9x2-16y2(a+b)(a-b)=a2-b2=(3x+4y)(3x-4y)平方差公式的应用1.两个因式中有一项完全相同,另一项互为相反数;2.一般符号相同的在前,符号不同的在后。(a+b)(a-b)=a2-b2平方差公式的应用(1)(x-y)(x+y)(2)(m+n)(m-n)(3)(a+2)(2-a)(4)(3y+x)(x-3y)平方差公式的应用解法1(-4a-1)(4a-1)解法2(-4a-1)(4a-1)=(-1-4a)(-1+4a)0=-(4a+1(4a-1)=(-1)2-(4a)2=-[(4a)2-12]=1-16a2=-(16a2-1)=1-16a2平方差公式的应用把-1看成一个数,把4a看成另一个数,调换位置后,直接写出(-1)2-(4a)2后得出结果.解法1(-4a-1)(4a-1)=(-1-4a)(-1+4a)=(-1)2-(4a)2=1-16a2-1-14a4a=(-1-4a)(-1+4a)=(-1)2-(4a)2平方差公式的应用解法2(-4a-1)(4a-1)=-(4a+1)(4a-1)=-[(4a)2-12]=-(16a2-1)=1-16a2解法2先了提出负号的办法,使两乘式首项变成正的,(-4a-1)应用平方差公式,写出结果.(1)(x+2y)(x-2y)(2)(3m-5n)(5n+3m)(3)(-1+x)(-1-x)(4)(-2b-5)(2b-5)(5)(x+1)(x-2)(6)(p+q)(p2+q2)(p-q)平方差公式的应用今天学到了什么?有什么收获?1什么是平方差公式?2运用公式要注意什么?(1)要符合公式特征才能运用平方差公式(2)有些式子表面不能应用公式,但实质能应用公式,要注意变形