6.13第六章 一次方程（组）和一次不等式（组） 复习课件.pptxVIP免费

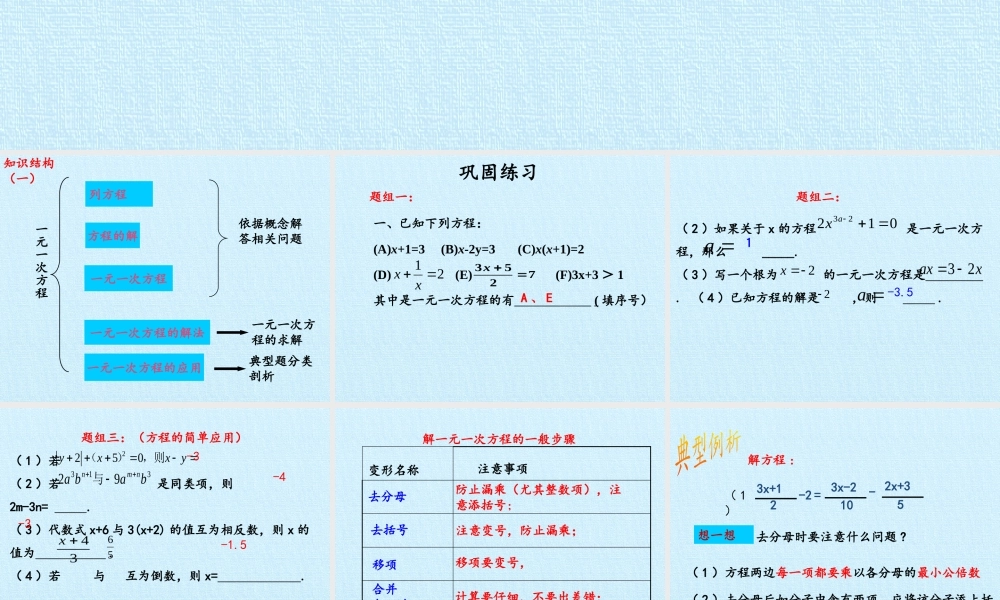
第六章一次方程（组）和一次不等式（组）复习课件知识结构（一）一元一次方程列方程一元一次方程一元一次方程的解法一元一次方程的应用依据概念解答相关问题一元一次方程的求解典型题分类剖析方程的解一、已知下列方程：(A)x+1=3(B)x-2y=3(C)x(x+1)=2(D)(E)(F)3x+3＞1其中是一元一次方程的有(填序号）7253x21xxA、E巩固练习题组一：（2）如果关于x的方程是一元一次方程，那么_____.（3）写一个根为的一元一次方程是.（4）已知方程的解是，则.题组二：１-3.501223axa2xxax232xa题组三：（方程的简单应用）（1）若（2）若是同类项，则2m-3n=.（3）代数式x+6与3(x+2)的值互为相反数，则x的值为.（4）若与互为倒数，则x=.2250yxxy（），则31392babanmn与34x56-3-4-1.5-3解一元一次方程的一般步骤变形名称注意事项去分母去括号移项合并(ax=b)系数化成1防止漏乘（尤其整数项），注意添括号；注意变号，防止漏乘；移项要变号，计算要仔细，不要出差错；计算要仔细，分子分母不要颠倒解方程:23x+1-2103x-252x+3=-去分母时要注意什么问题?（1）方程两边每一项都要乘以各分母的最小公倍数（2）去分母后如分子中含有两项,应将该分子添上括号想一想（1）解：211012121364xxx（）4(2x–1）–2(10x+1）=3(2x+1）–128x–4–20x–2=6x+3–128x–20x–6x=4+2+3–12–18x=–3x=16解：0a时，abx方程有唯一解时，0a0b若，则方程有无数解0b若，则方程无解bax1.解关于X的方程：235x解：当5x-3≥0时，原方程可化为：235x15x55x532x（）1x51x2.解方程：当5x-30﹤时，原方程可化为：列方程解应用题的步骤：1.审题：理解题意，弄清已知量、未知量及它们之间的关系2.设元：选择适当的未知数，可直接设元，也可间接设元（设元的语句必须完整，并包括元素名称及单位）3.列方程：用含未知数的式子表示问题中的相等关系4.解方程:解所列方程,准确求出未知数的值5.写答案:检验所列方程的解,符合题意后,写出答案,并注明单位名称abx列方程中常见的实际问题中的等量关系：1.行程问题:路程=时间×速度2.工程问题:工作总量=工作效率×工作时间3.浓度问题:溶质质量=溶液质量×溶液浓度4.营销问题:商品利润=商品进价×商品利润率(或商品利润=商品售价－商品进价)5.水上航行中的有关量之间的关系:逆水速度=船在静水中的速度－水速顺水速度=船在静水中的速度＋水速6.数字数位问题:数...