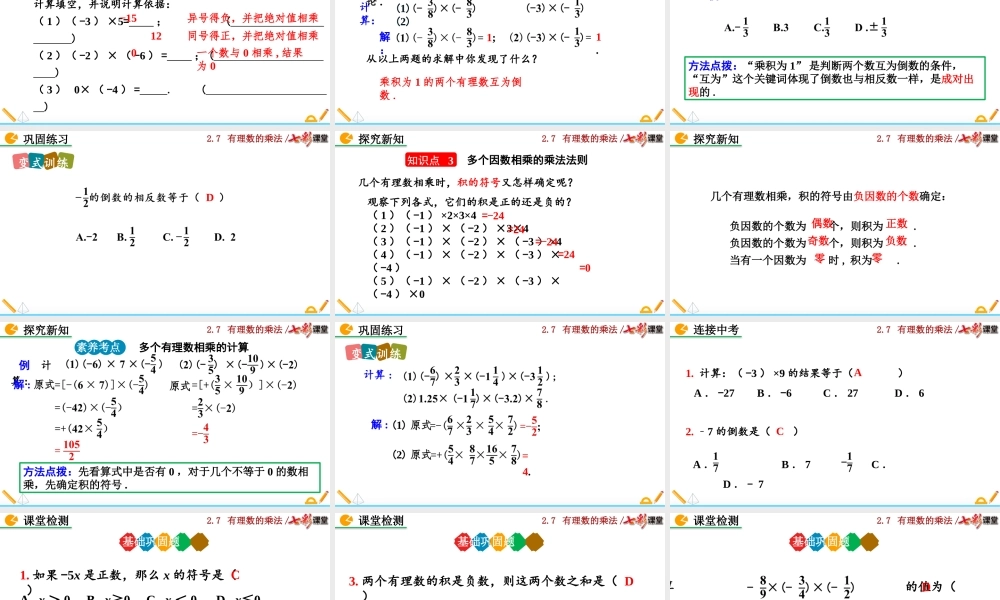
2.7有理数的乘法/2.7有理数的乘法(第1课时)北师大版数学七年级上册2.7有理数的乘法/素养目标2.理解倒数的含义.1.理解有理数乘法的意义,掌握有理数乘法法则中积的符号法则,并初步理解有理数乘法法则的合理性.3.能根据有理数乘法法则熟练地进行有理数乘法运算,掌握多个有理数相乘的积的符号法则.2.7有理数的乘法/导入新知如图一只蜗牛沿直线爬行,它现在的位置恰在l上的点O处,如果用正号表示向右,用负号表示向左.请思考后回答下面的问题:(1)如果蜗牛一直以2cm/min的速度向右爬行,3min后它在什么位置?(2)如果蜗牛一直以2cm/min的速度向左爬行,3min后它在什么位置?我们能否用数学式子来表示呢?2×3=6(-2)×3=-62.7有理数的乘法/探究新知知识点1有理数的乘法法则想一想甲水库的水位每天升高3cm,乙水库的水位每天下降3cm,4天后甲、乙水库水位的总变化量各是多少?甲水库第一天乙水库第二天第三天第四天第一天第二天第三天第四天2.7有理数的乘法/如果用正号表示水位的上升,用负号表示水位的下降,那么4天后,甲水库的水位总变化量为3+3+3+3=3×4=12(cm);(−3)+(−3)+(−3)+(−3)=(−3)×4=−12(cm).乙水库的水位总变化量为探究新知2.7有理数的乘法/探究新知(-3)×4=你能写出下列结果吗?(-3)×(-1)=-9,-6,-3,0.3,6,9,12.(-3)×3=(-3)×2=(-3)×1=(-3)×0=(-3)×(-2)=(-3)×(-3)=(-3)×(-4)=-12,议一议左边各题的结果是多少?一个因数减小1时,积怎样变化?当一个因数减小1时,积增大3.2.7有理数的乘法/探究新知观察以下算式中因数的符号和积的符号,你认为有怎样的规律?同号相乘,结果为正.异号相乘,结果为负.与0相乘,结果为0.(-3)×3=-9(-3)×2=-6(-3)×1=-3(-3)×0=0(-3)×(-1)=3(-3)×(-2)=6(-3)×(-3)=92.7有理数的乘法/做一做计算:异号得负,绝对值相乘同号得正,绝对值相乘解:(1)原式(2)原式(3)原式与0相乘,结果为0(1)(-3)×6=-(3×6)=-18(2)=0探究新知2.7有理数的乘法/探究新知两数相乘,同号得正,异号得负,并把绝对值相乘.有理数乘法法则任何数与0相乘,积仍为0.2.7有理数的乘法/例计算:素养考点运用有理数乘法法则计算解:方法点拨:第一步是确定积的符号;第二步是确定积的绝对值.(4)(-2)×6=-12.(1)(-5)×(+3)=-5×3=-15;(2)(-8)×(-7)=8×7=56;探究新知2.7有理数的乘法/计算填空,并说明计算依据:(1)(-3)×5=;()(2)(-2)×(-6)=;()(3)0×(-4)=.()...