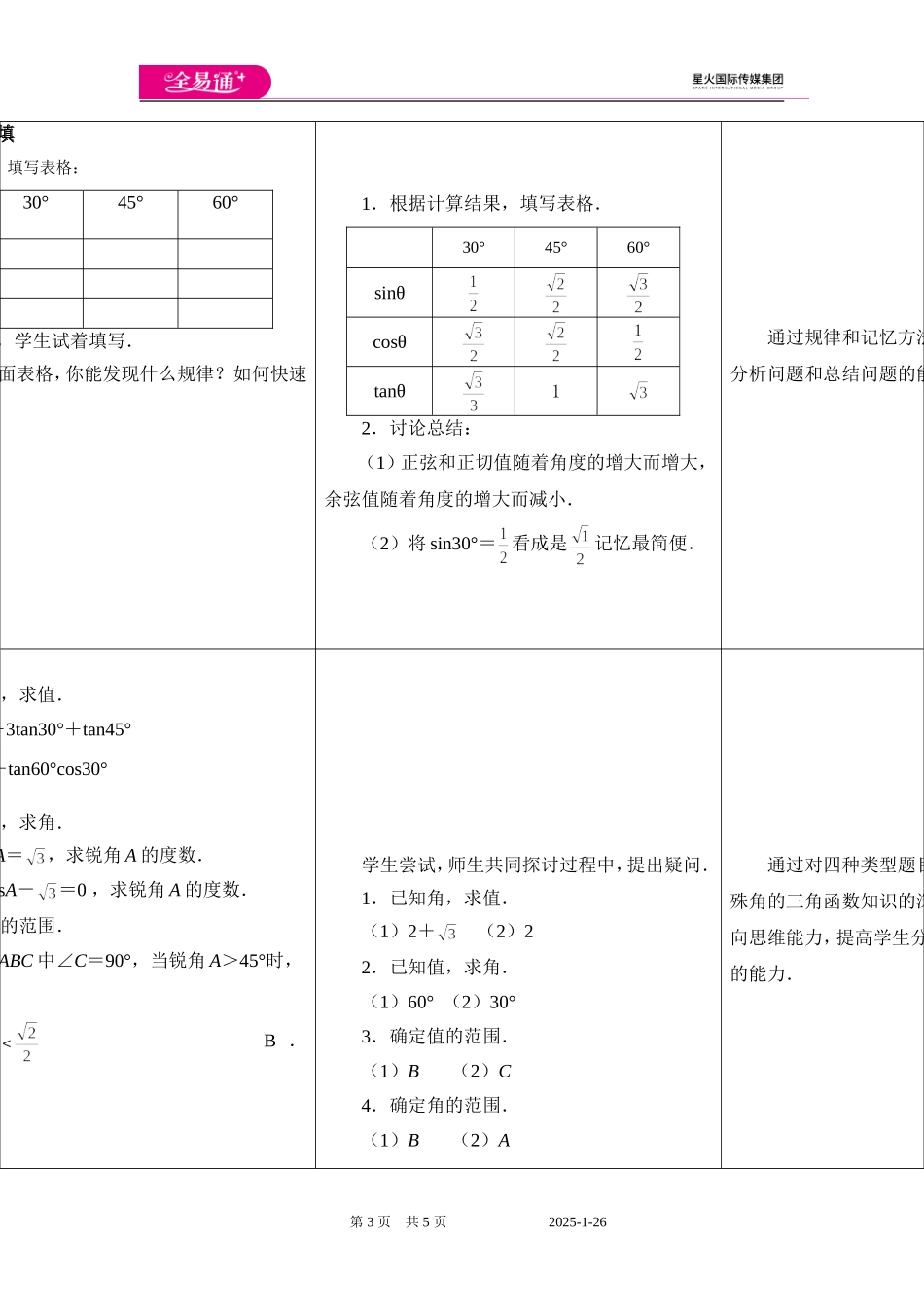
7.3特殊角的三角函数1.能通过推理得30°、45°、60°角的三角函数值,进一步体会三角函数的意义;2.会计算含有30°、45°、60°角的三角函数值;3.能根据30°、45°、60°角的三角函数值,说出相应锐角的大小;4.经历探索30°、45°、60°角的三角函数值的过程,发展学生推理能力和计算能力.通过推理得30°、45°、60°角的三角函数值,进一步体会三角函数的意义.特殊角的三角函数的运用.教学过程(教师)学生活动设计思路知新BC中,∠C为直角,如何表示∠A的三,根据学生回答,同时板书.弦独立思考,回答教师出示的问题.通过对三角函数知识特殊角的三角函数的学习想0°、45°、60°角的三角函数值吗?计算器计算,是否可以通过手里的三角其他的方法呢?讨论得到结论:1.利用计算器计算.2.利用三角尺的特殊角,量出各边的长度,再用定义计算.通过用计算器的计算三角板中存在特殊角的计引导,让学生感受数学方学生的思维创新,从而加解.试学生独立思考,回答问题:第1页共5页2025-1-26ACB中,∠C=90°,∠A=30°.:AB:AC=();1,则AC=()AB=();sin30°,cos30°,tan30°的函数值吗?CB成30°角的三角函数值的求解过程,并总结.你能求出sin45°,cos45°,tan45°的函数你能求出它的三角函数值吗?书,师生共同评价.1.请说出BC:AB:AC=1:2:;2.若设BC=1,则AC=,AB=2;3.你能求出sin30°,cos30°,tan30°的函数值吗?sin30°=,cos30°=,tan30°=总结:设直角三角形一边的长为某个常数,求出另外两边的长,再利用定义进行计算;选择最简单的数据计算.板书:sin45°=,cos45°=,tan45°=1,sin60°=,cos60°=,tan60°=.师生共同评价.在学生最近发展区设让学生掌握求30°角的三通过对求30°角的三给学生求解的方法,并学据进行计算,并将此种60°角的求解过程.第2页共5页2025-1-26填填写表格:30°45°60°,学生试着填写.面表格,你能发现什么规律?如何快速1.根据计算结果,填写表格.30°45°60°sinθcosθtanθ12.讨论总结:(1)正弦和正切值随着角度的增大而增大,余弦值随着角度的增大而减小.(2)将sin30°=看成是记忆最简便.通过规律和记忆方法分析问题和总结问题的能,求值.+3tan30°+tan45°+tan60°cos30°,求角.A=,求锐角A的度数.sA-=0,求锐角A的度数.的范围.ABC中∠C=90°,当锐角A>45°时,B.学生尝试,师生共同探讨过程中,提出疑问.1.已知角,求值.(1)2...