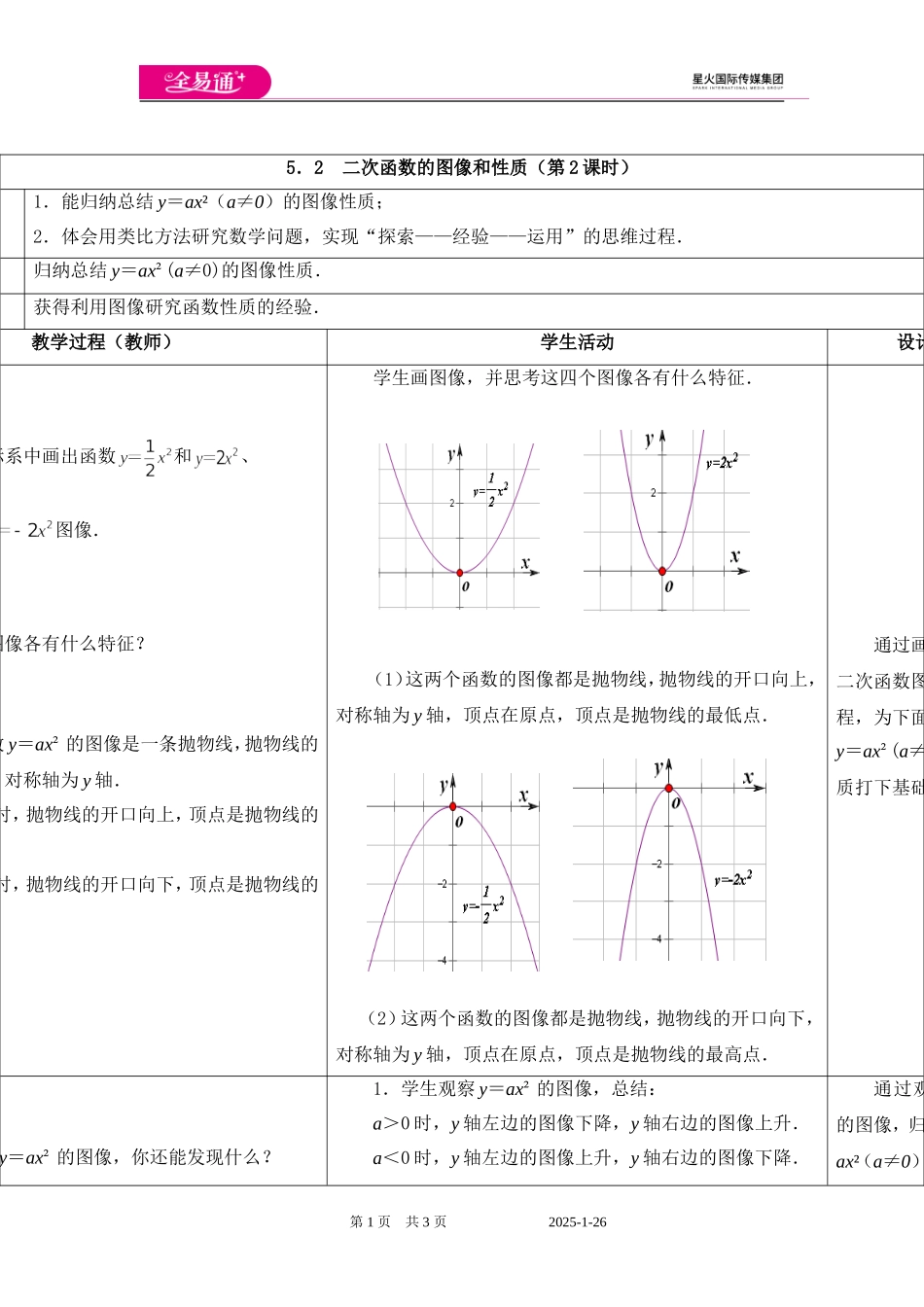
5.2二次函数的图像和性质(第2课时)1.能归纳总结y=ax²(a≠0)的图像性质;2.体会用类比方法研究数学问题,实现“探索——经验——运用”的思维过程.归纳总结y=ax²(a≠0)的图像性质.获得利用图像研究函数性质的经验.教学过程(教师)学生活动设计标系中画出函数和、图像.图像各有什么特征?数y=ax²的图像是一条抛物线,抛物线的对称轴为y轴.时,抛物线的开口向上,顶点是抛物线的时,抛物线的开口向下,顶点是抛物线的学生画图像,并思考这四个图像各有什么特征.(1)这两个函数的图像都是抛物线,抛物线的开口向上,对称轴为y轴,顶点在原点,顶点是抛物线的最低点.(2)这两个函数的图像都是抛物线,抛物线的开口向下,对称轴为y轴,顶点在原点,顶点是抛物线的最高点.通过画二次函数图程,为下面y=ax²(a≠质打下基础y=ax²的图像,你还能发现什么?1.学生观察y=ax²的图像,总结:a>0时,y轴左边的图像下降,y轴右边的图像上升.a<0时,y轴左边的图像上升,y轴右边的图像下降.通过观的图像,归ax²(a≠0)第1页共3页2025-1-26用x、y的值的变化来描述图像的上升、下>0时,,y随x的增大而减小;,y随x的增大而增大;,y有最小值,最小值为0.0时,,y随x的增大而增大;,y随x的增大而减小;,y有最大值,最大值为0.2.学生用x、y的值的变化来描述图像的上升、下降:a>0时,由y轴左边的图像下降可以知道:当x<0时,随着x增大y减小.a<0时,由y轴左边的图像上升可以知道:当x<0时,随着x增大y增大.培养学生运一般”总结思想.出下列函数图像的开口方向、顶点坐标、减性、最值.-3x²;(2)y=0.6x²;0.75x²;(4)y=-100x².学生利用y=ax²(a≠0)的图像与性质回答所给函数的相关性质.通过说进一步加深y=ax²(a≠质的认识.知函数是二次函数且其下,m的值和函数解析式.什么范围内,y随x的增大而增大;y随x小.1.学生完成例题,并在小组内交流.2.学生展示解决问题的方法.例1解:(1)由题意知:m-1<0且m²+m=2,则m=-2.(2)当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.例2解:通过两加强学生对(a≠0)图识.第2页共3页2025-1-26数y=y=ax²(a≠0)与直线y=2x-3交,求:b的值.物线y=ax²的解析式,并求顶点坐标和对(1)将A(1,b)代入y=2x-3,得:b=-1;将A(1,-1)代入y=ax²(a≠0),得:a=-1.(2)抛物线:y=-x²;顶点(0,0);对称轴:y轴.课中...