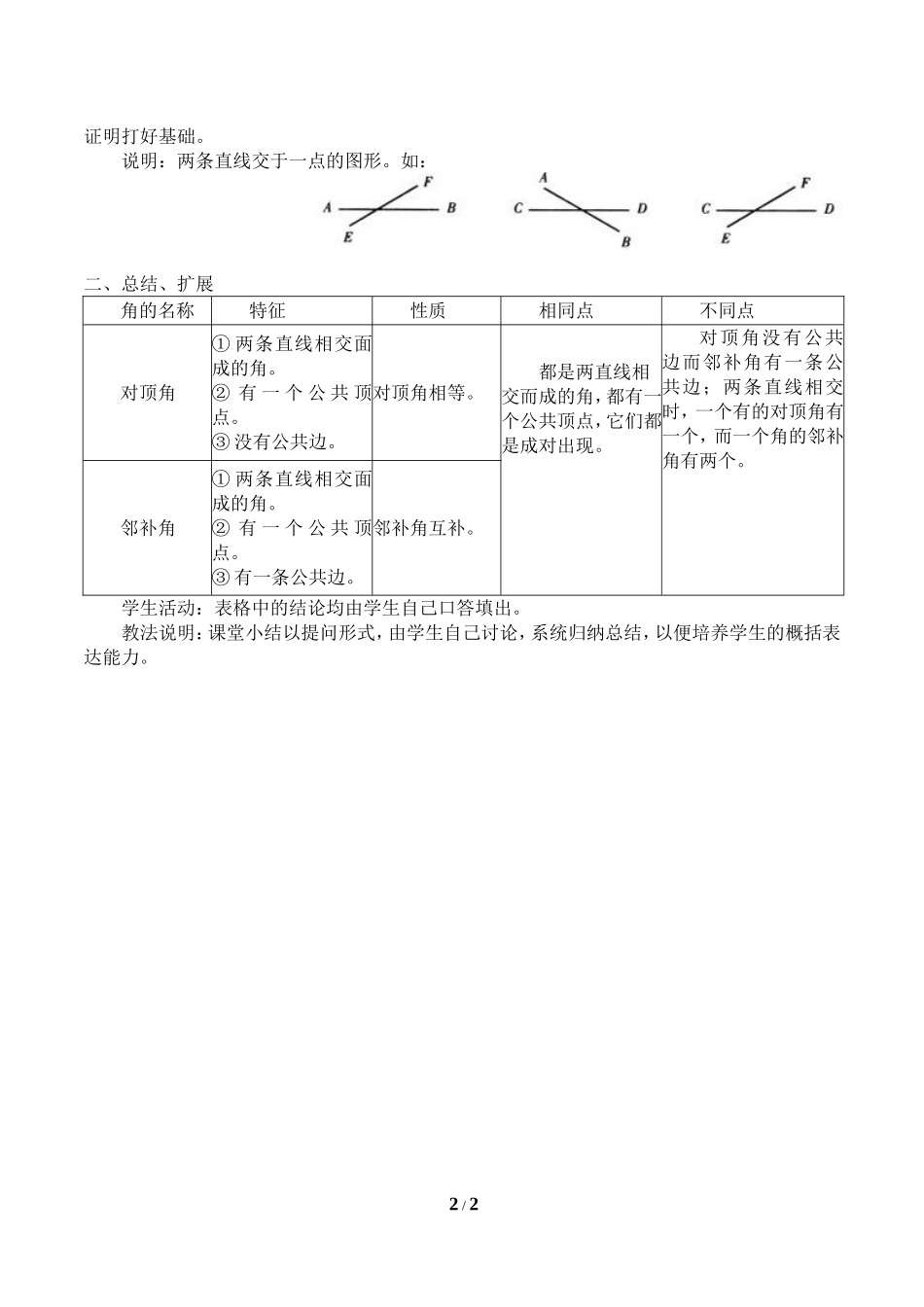
邻补角、对顶角【教学目标】1.理解对顶角和邻补角的概念,能在图形中辨认。2.掌握对顶角相等的性质和它的推证过程。3.会用对顶角的性质进行有关的推理和计算。【教学重难点】1.通过在图形中辨认对顶角和邻补角,培养学生的识图能力。2.通过对顶角性质的推理过程,培养学生的推理和逻辑思维能力。【教学过程】一、新课导入邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角,由此可知,邻补角是有特殊位置关系的两个互补的角。下图这样的邻补角在图形中也是常见的。在这种情况下,只存在一对邻补角,而不存在对顶角,与两条直线相交所得的角不同。1.提出问题:∠l和∠2的和是多少度?∠l和∠2还是邻补角吗?为什么?教法说明:此问题意在区别互为补角和互为邻补角的概念,演示活动投影片,有助于学生抓住概念的本质,比教师单纯地强调效果更好。2.对顶角的性质提出问题:我们在图形中能准确地辨认对顶角,那么对顶角有什么性质呢?教法说明:学生说出对顶角∠l=∠3后,启发学生再说出∠2=∠4,然后得出对顶角相等的性质。在学生理解推理思路的基础上,进行推理。对顶角的性质不难得出,放手让学生展开讨论,充分发挥学生的主动性,培养学生的创造思维能力。因为∠1与∠2互补,∠3与∠2互补(邻补角定义),所以∠l=∠3(同角的补角相等)。(注意:∠l与∠2互补不是给出的已知条件,而是分析图形得到的;所以括号内不填已知,而是填邻补角定义。)或写成:所以∠1=180°-∠2,∠3=180°-∠2(邻补角定义),所以∠1=∠3。教法说明:推得“对顶角相等”这个结论的过程,是课本中出现的一步推理,使学生了解推理可以写成的形式,并且每一步都要有根据,也就是括号里填的理由。这种推理的格式以后还要逐步渗透和训练,现在不要求自己会写推理过程,只要求学生能看明白就可以了,为以后1/2证明打好基础。说明:两条直线交于一点的图形。如:二、总结、扩展角的名称特征性质相同点不同点对顶角①两条直线相交面成的角。②有一个公共顶点。③没有公共边。对顶角相等。都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现。对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个有的对顶角有一个,而一个角的邻补角有两个。邻补角①两条直线相交面成的角。②有一个公共顶点。③有一条公共边。邻补角互补。学生活动:表格中的结论均由学生自己口答填出。教法说明:课堂小结以提问形式,由学生自己讨论,...