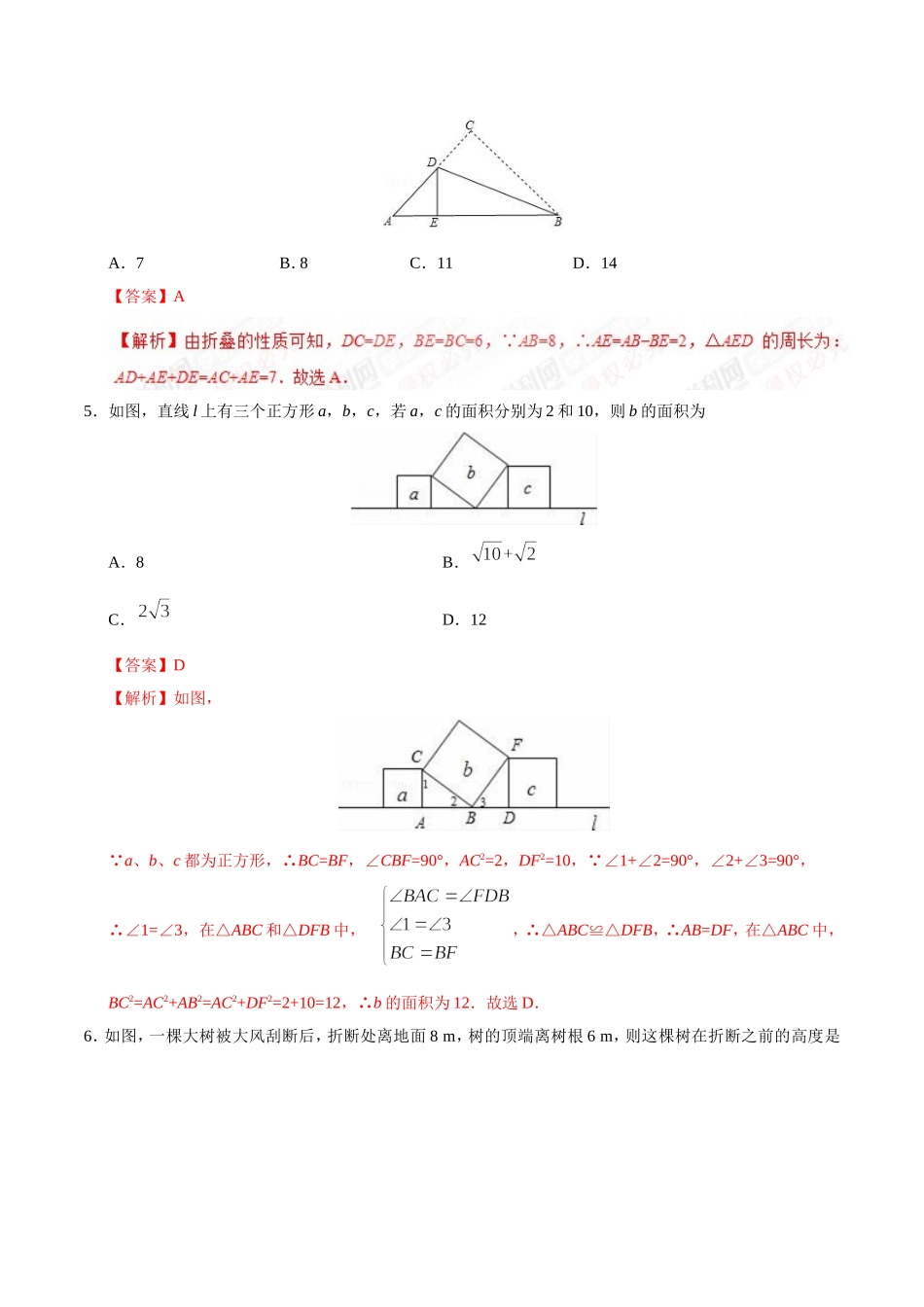
第十七章勾股定理17.1勾股定理一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.一个直角三角形有两条边长分别为6和8,则它的第三条边长可能是A.8B.9C.10D.11【答案】C2.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为A.8B.4C.6D.无法计算【答案】A【解析】利用勾股定理,由Rt△ABC中,BC为斜边,可得AB2+AC2=BC2,代入数据可得AB2+AC2+BC2=2BC2=2×22=8.故选A.3.如图,在四边形ABCD中,∠BAD=90°,∠DBC=90°,AD=4,AB=3,BC=12,则CD为A.5B.13C.17D.18【答案】B【解析】 ∠BAD=90°,∴△ADB是直角三角形,∴BD===5, ∠DBC=90°,∴△DBC是直角三角形,∴CD===13,故选B.4.如图的三角形纸片中,AB=8,BC=6,AC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长是A.7B.8C.11D.14【答案】A5.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为2和10,则b的面积为A.8B.C.D.12【答案】D【解析】如图, a、b、c都为正方形,∴BC=BF,∠CBF=90°,AC2=2,DF2=10, ∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3,在△ABC和△DFB中,,∴△ABC≌△DFB,∴AB=DF,在△ABC中,BC2=AC2+AB2=AC2+DF2=2+10=12,∴b的面积为12.故选D.6.如图,一棵大树被大风刮断后,折断处离地面8m,树的顶端离树根6m,则这棵树在折断之前的高度是A.18mB.10mC.14mD.24m【答案】A【解析】 BC=8m,AC=6m,∠C=90º,∴AB=m,∴树高10+8=18m.故选A.7.如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是A.6cmB.7cmC.8cmD.9cm【答案】B8.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为A.B.C.D.【答案】C【解析】S△ABC=×BC×AE=×BD×AC, AE=4,AC==5,BC=4,即×4×4=×5×BD,解得BD=.故选C.二、填空题:请将答案填在题中横线上.9.已知在△ABC中,AB=9,AC=10,BC=17,那么边AB上的高等于__________.【答案】8【解析】如图,作CD⊥AB交AB的延长线于D点,设CD=x,AD=y,在直角△ADC中,AC2=x2+y2,在直角△BDC中,BC2=x2+(y+AB)2,解方程得y=6,x=8,即CD=8, CD即AB边上的高,∴AB边上的高等于8.故答案为:8.10.如图,在△ABC中,∠C=90°,AC=6,AB=10,现分别以A、B为圆心,大于AB长为半径作弧,两弧相交于点M、N,作直线MN,分别交AB、BC于点D、E,则CE的长为__________.【答案】11.如图,在△ABC...