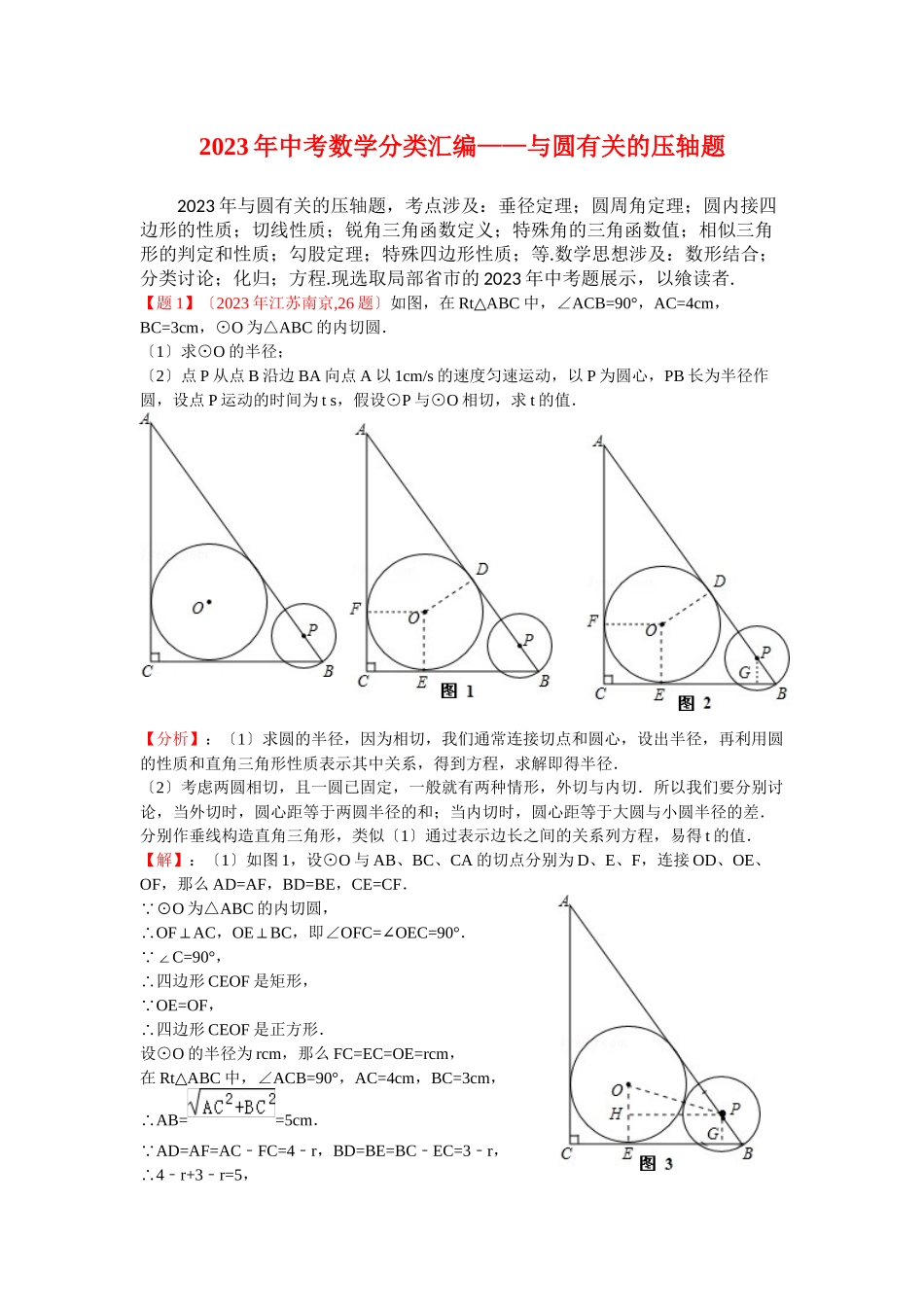
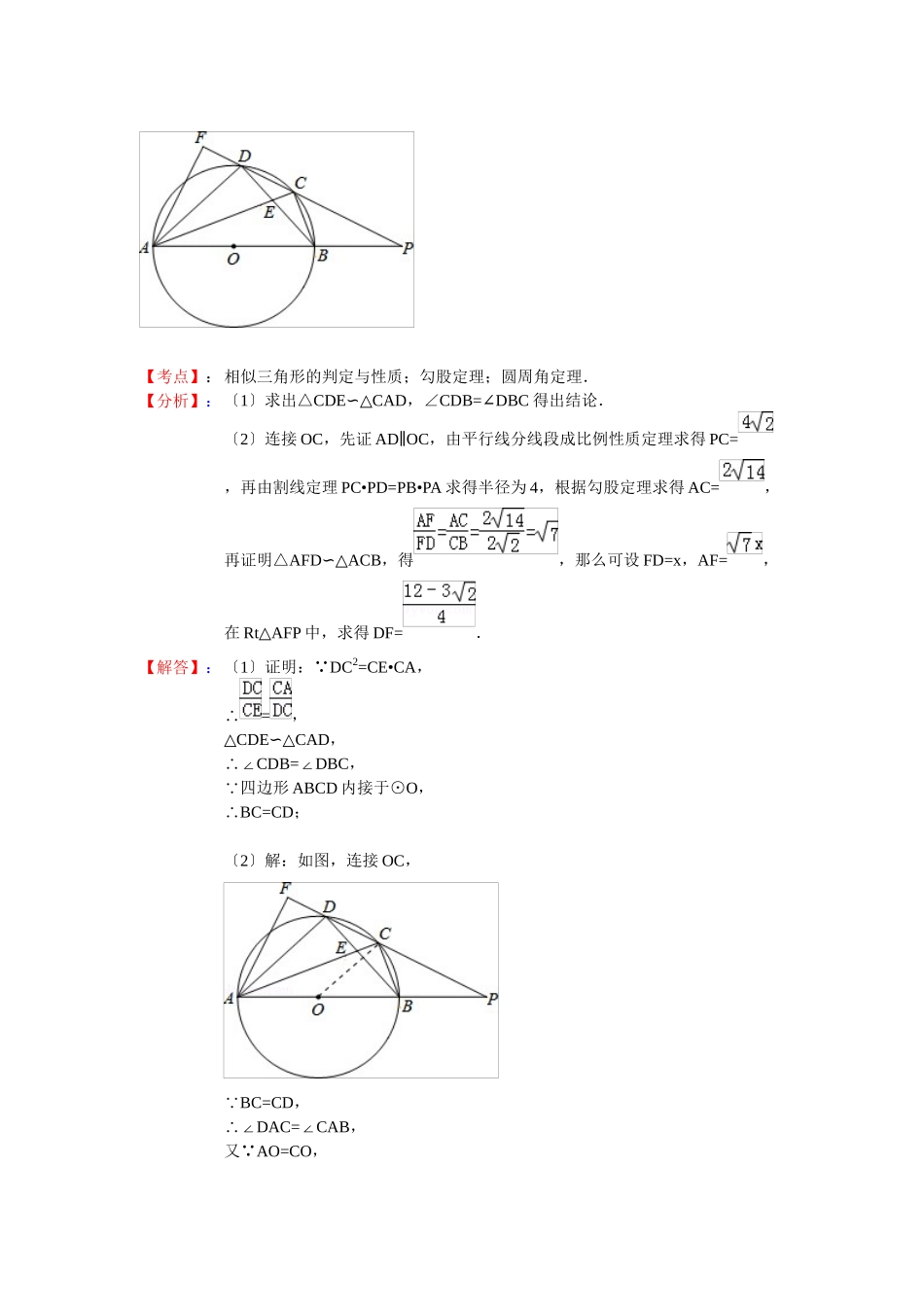
2023年中考数学分类汇编——与圆有关的压轴题2023年与圆有关的压轴题,考点涉及:垂径定理;圆周角定理;圆内接四边形的性质;切线性质;锐角三角函数定义;特殊角的三角函数值;相似三角形的判定和性质;勾股定理;特殊四边形性质;等.数学思想涉及:数形结合;分类讨论;化归;方程.现选取局部省市的2023年中考题展示,以飨读者.【题1】〔2023年江苏南京,26题〕如图,在RtABC△中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.〔1〕求⊙O的半径;〔2〕点P从点B沿边BA向点A以1cm/s的速度匀速运动,以P为圆心,PB长为半径作圆,设点P运动的时间为ts,假设⊙P与⊙O相切,求t的值.【分析】:〔1〕求圆的半径,因为相切,我们通常连接切点和圆心,设出半径,再利用圆的性质和直角三角形性质表示其中关系,得到方程,求解即得半径.〔2〕考虑两圆相切,且一圆已固定,一般就有两种情形,外切与内切.所以我们要分别讨论,当外切时,圆心距等于两圆半径的和;当内切时,圆心距等于大圆与小圆半径的差.分别作垂线构造直角三角形,类似〔1〕通过表示边长之间的关系列方程,易得t的值.【解】:〔1〕如图1,设⊙O与AB、BC、CA的切点分别为D、E、F,连接OD、OE、OF,那么AD=AF,BD=BE,CE=CF.O ⊙为△ABC的内切圆,OFAC∴⊥,OEBC⊥,即∠OFC=OEC=90°∠.C=90° ∠,∴四边形CEOF是矩形,OE=OF ,∴四边形CEOF是正方形.设⊙O的半径为rcm,那么FC=EC=OE=rcm,在RtABC△中,∠ACB=90°,AC=4cm,BC=3cm,AB=∴=5cm.AD=AF=ACFC=4r ﹣﹣,BD=BE=BCEC=3r﹣﹣,4r+3r=5∴﹣﹣,解得r=1,即⊙O的半径为1cm.〔2〕如图2,过点P作PGBC⊥,垂直为G.PGB=C=90° ∠∠,∴PGAC∥.PBGABC∴△∽△,∴. BP=t,PG=∴,BG=.假设⊙P与⊙O相切,那么可分为两种情况,⊙P与⊙O外切,⊙P与⊙O内切.①当⊙P与⊙O外切时,如图3,连接OP,那么OP=1+t,过点P作PHOE⊥,垂足为H.PHE=HEG=PGE=90° ∠∠∠,∴四边形PHEG是矩形,HE=PG∴,PH=CE,OH=OEHE=1∴﹣﹣,PH=GE=BCECBG=31﹣﹣﹣﹣=2﹣.在RtOPH△中,由勾股定理,,解得t=.②当⊙P与⊙O内切时,如图4,连接OP,那么OP=t1﹣,过点O作OMPG⊥,垂足为M.MGE=OEG=OMG=90° ∠∠∠,∴四边形OEGM是矩形,MG=OE∴,OM=EG,PM=PGMG=∴﹣,OM=EG=BCECBG=31﹣﹣﹣﹣=2﹣,在RtOPM△中,由勾股定理,,解得t=2.综上所述,⊙P与⊙O相切时,t=s或t=2s.【点评】:此题考查了圆的性质、两圆相切及通过设边长,表...