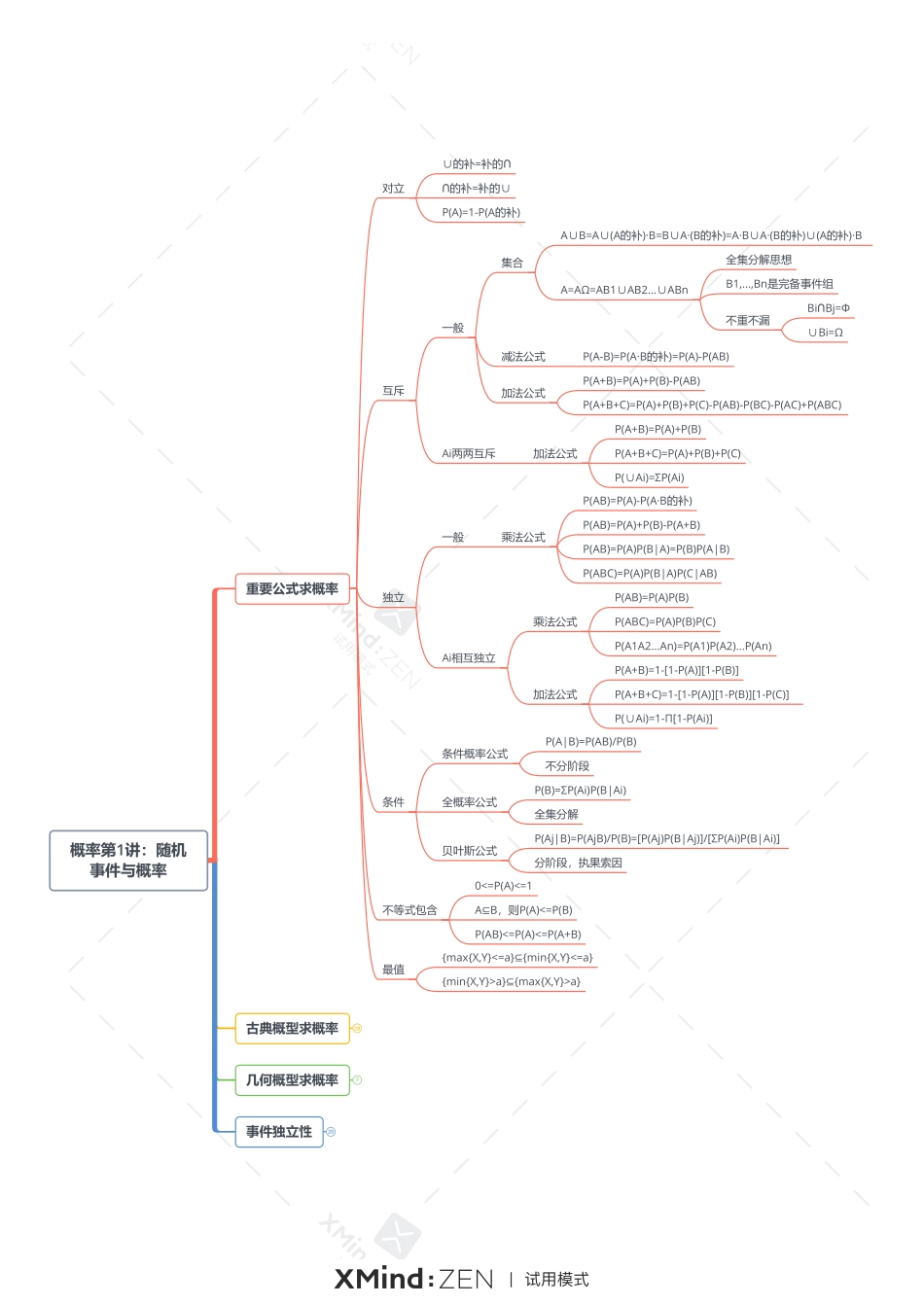
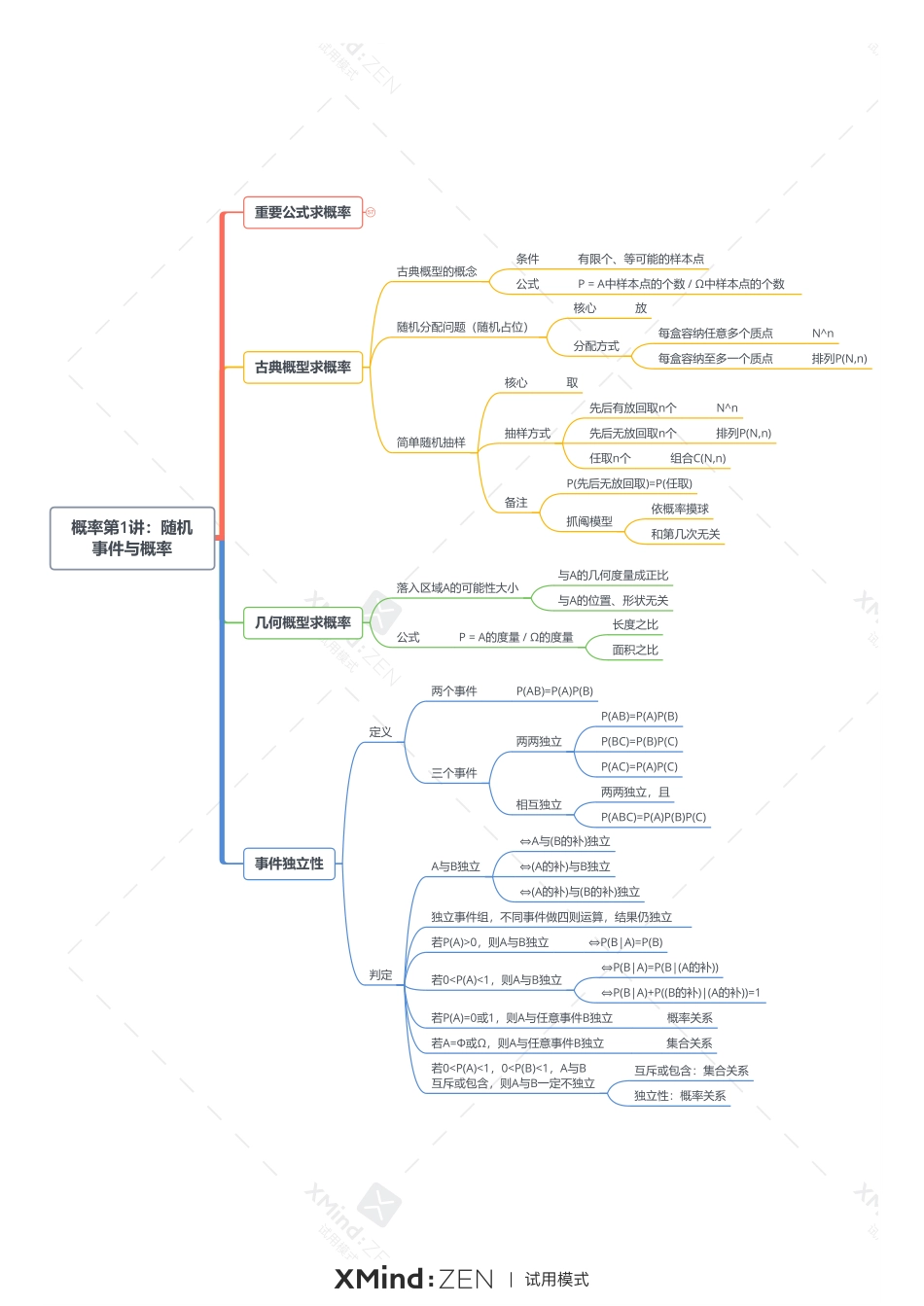
概率第1讲:随机事件与概率古典概型求概率28几何概型求概率7事件独立性29重要公式求概率对立∪的补=补的∩∩的补=补的∪P(A)=1-P(A的补)互斥一般集合A∪B=A∪(A的补)·B=B∪A·(B的补)=A·B∪A·(B的补)∪(A的补)·BA=AΩ=AB1∪AB2...∪ABn全集分解思想B1,...,Bn是完备事件组不重不漏Bi∩Bj=Φ∪Bi=Ω减法公式P(A-B)=P(A·B的补)=P(A)-P(AB)加法公式P(A+B)=P(A)+P(B)-P(AB)P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)Ai两两互斥加法公式P(A+B)=P(A)+P(B)P(A+B+C)=P(A)+P(B)+P(C)P(∪Ai)=ΣP(Ai)独立一般乘法公式P(AB)=P(A)-P(A·B的补)P(AB)=P(A)+P(B)-P(A+B)P(AB)=P(A)P(B|A)=P(B)P(A|B)P(ABC)=P(A)P(B|A)P(C|AB)Ai相互独立乘法公式P(AB)=P(A)P(B)P(ABC)=P(A)P(B)P(C)P(A1A2...An)=P(A1)P(A2)...P(An)加法公式P(A+B)=1-[1-P(A)][1-P(B)]P(A+B+C)=1-[1-P(A)][1-P(B)][1-P(C)]P(∪Ai)=1-Π[1-P(Ai)]条件条件概率公式P(A|B)=P(AB)/P(B)不分阶段全概率公式P(B)=ΣP(Ai)P(B|Ai)全集分解贝叶斯公式P(Aj|B)=P(AjB)/P(B)=[P(Aj)P(B|Aj)]/[ΣP(Ai)P(B|Ai)]分阶段,执果索因不等式包含0<=P(A)<=1A⊆B,则P(A)<=P(B)P(AB)<=P(A)<=P(A+B)最值{max{X,Y}<=a}⊆{min{X,Y}<=a}{min{X,Y}>a}⊆{max{X,Y}>a}概率第1讲:随机事件与概率古典概型求概率几何概型求概率事件独立性随机分配问题(随机占位)核心简单随机抽样分配方式放每盒容纳任意多个质点每盒容纳至多一个质点N^n排列P(N,n)古典概型的概念条件公式有限个、等可能的样本点P=A中样本点的个数/Ω中样本点的个数核心取抽样方式先后有放回取n个N^n先后无放回取n个任取n个排列P(N,n)组合C(N,n)备注P(先后无放回取)=P(任取)抓阄模型依概率摸球和第几次无关公式P=A的度量/Ω的度量落入区域A的可能性大小与A的几何度量成正比与A的位置、形状无关长度之比面积之比定义判定两个事件三个事件P(AB)=P(A)P(B)两两独立相互独立P(AB)=P(A)P(B)P(BC)=P(B)P(C)P(AC)=P(A)P(C)两两独立,且P(ABC)=P(A)P(B)P(C)A与B独立独立事件组,不同事件做四则运算,结果仍独立⇔A与(B的补)独立⇔(A的补)与B独立⇔(A的补)与(B的补)独立若P(A)>0,则A与B独立若0