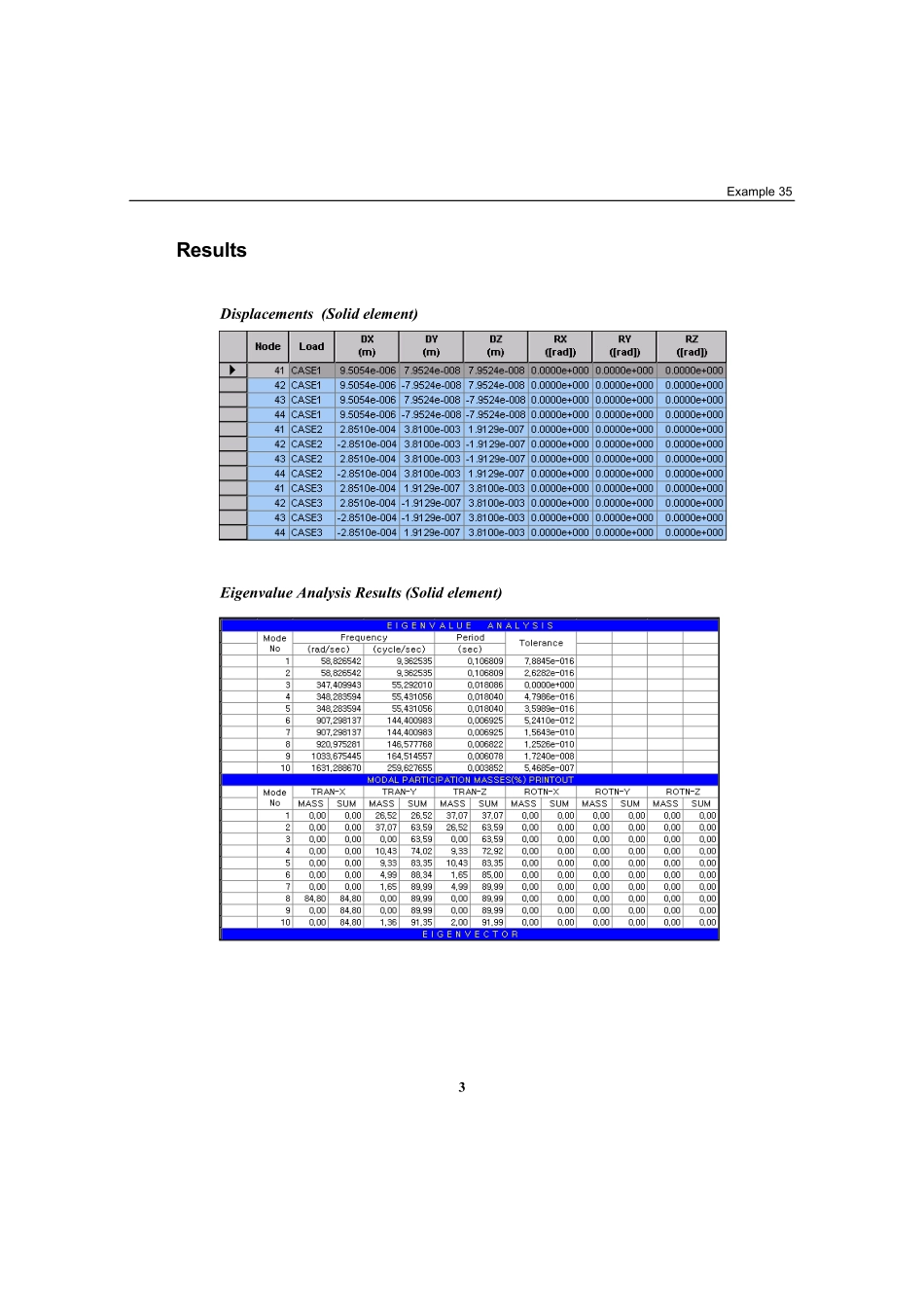
1Example35TitleBehaviorsofacantileverbeamunderconcentratedloadsatthefreeendDescriptionExaminethestatic&dynamicbehaviorsofacantileverbeam.Comparetheresultsbasedonthemodelscomposedofsolidelementsandbeamelements.StructuralanalysismodelandloadcasesVerificationExample2ModelAnalysisType3-DeigenvalueanalysisUnitSystemm,tonfDimensionLength5mElementSolidelementMaterialConcreteModulusofelasticityE=2.1×106tonf/m2Poisson’sratioν=0.167Weightdensityγ=2.4tonf/m3BoundaryConditionNodes1,2,3and4;ConstrainallDOFs.LoadCaseAconcentratedload,1tonfisappliedtoeachofthenodes41,42,43and44atthefreeend.Theloadcases1,2and3representtheloadsactinginthedirectionsofX,YandZrespectively.AnalysisCaseSelfweightisconvertedtonodalmassesautomatically.Numberofnaturalfrequenciestobecomputed=10Example353ResultsDisplacements(Solidelement)EigenvalueAnalysisResults(Solidelement)VerificationExample4ComparisonofResultsDisplacementsUnit:mLoadCaseNISAII(Solidelements)MIDAS/Gen(Beamelements)MIDAS/Gen(Solidelements)LDC1(Xdirection)9.505E-069.524E-069.505E-06LDC2(Ydirection)0.0038100.0038360.003810LDC3(Zdirection)0.0038100.0038360.003810NaturalPeriodsUnit:secNaturalPeriodNISAII(Solidelements)MIDAS/Gen(Beamelements)MIDAS/Gen(Solidelements)1stmode0.10680870.10672120.10680974thmode0.01804040.01775760.01804046thmode0.00692520.00671330.00692528thmode0.00682230.00683480.0068223ReferenceTomasJ.R.Hughes,“TheFiniteElementMethod”,Chapter3