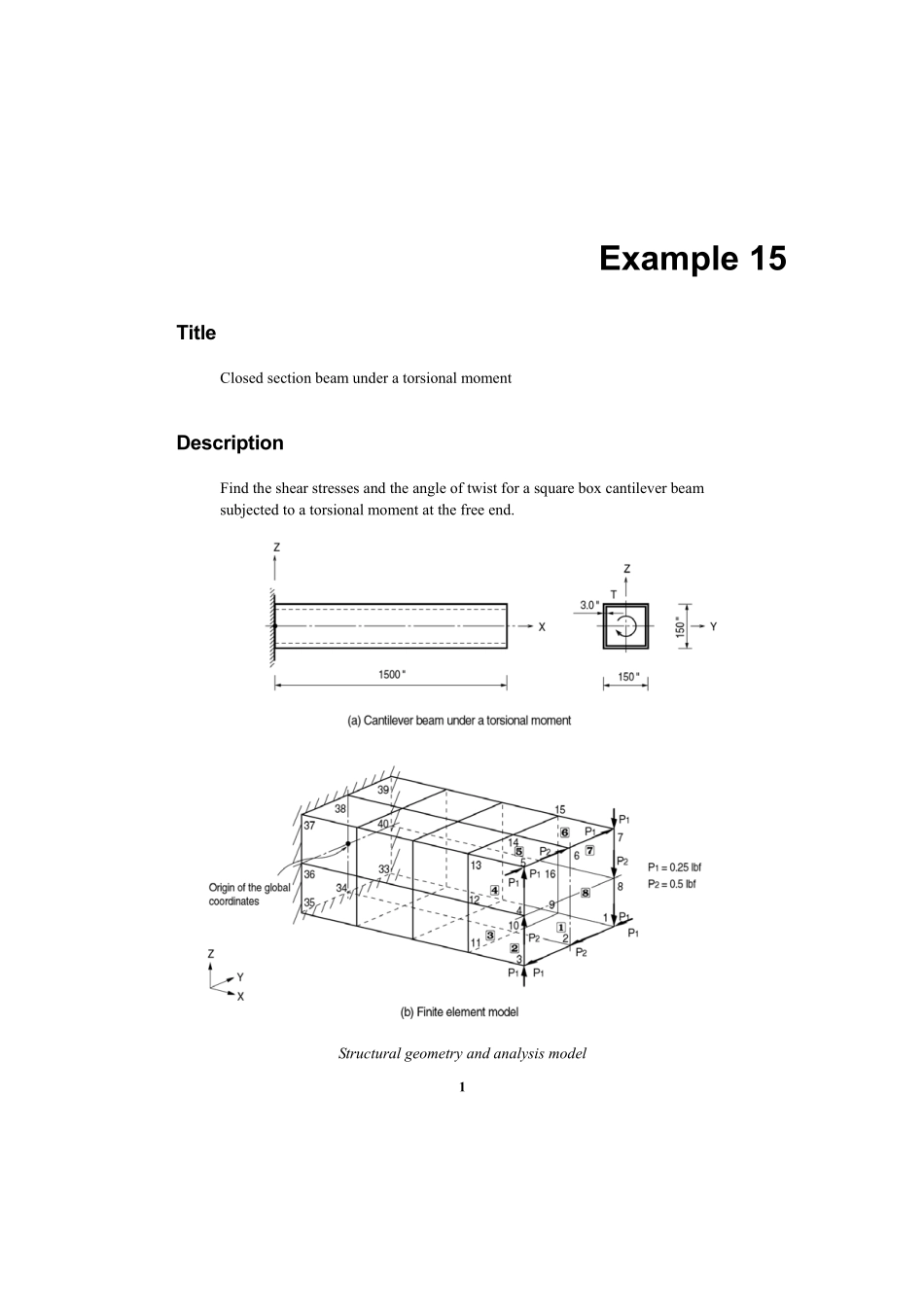
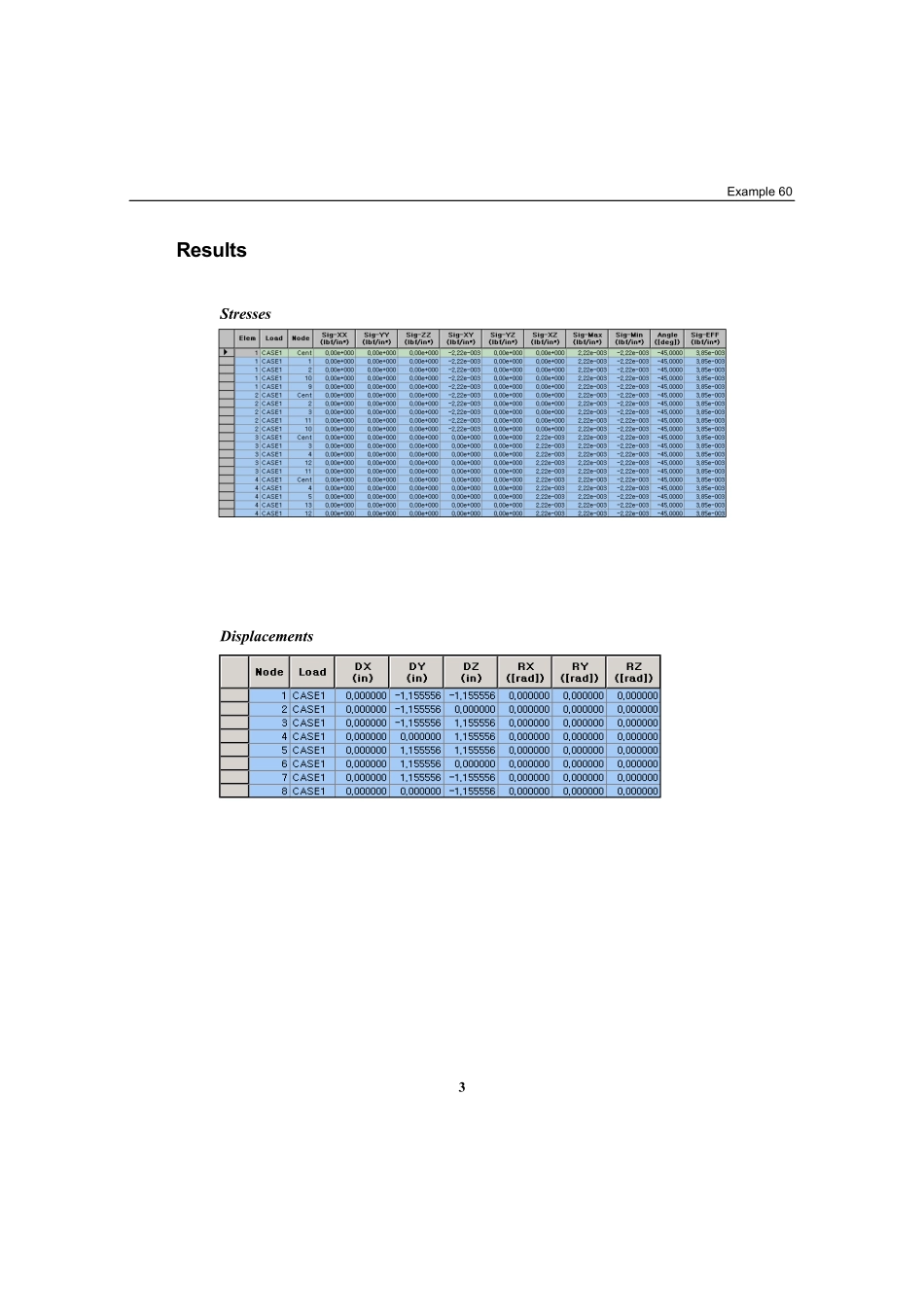
1Example15TitleClosedsectionbeamunderatorsionalmomentDescriptionFindtheshearstressesandtheangleoftwistforasquareboxcantileverbeamsubjectedtoatorsionalmomentatthefreeend.Structuralgeometryandanalysismodel2ModelAnalysisType3-DstaticanalysisUnitSystemin,lbfDimensionLength1500inWidth150inDepth150inElementPlanestresselementMaterialModulusofelasticityE=7.5psiPoisson’sratioν=0.3ElementPropertySizea×b=375in×75inThicknesst=3inBoundaryConditionNodes33~40;ConstrainallDOFs.LoadCaseTorsionalmomentisappliedtothefreeend,expressedintermsofequivalentcouples.Torsionalmoment=300.0lbf-inEquivalentloads,P1=0.25lbfandP2=0.5lbf(Refertothefigureshownabove)Example603ResultsStressesDisplacements4ComparisonofResultsTheoreticalcalculationShearstress(τxy)=taT22=0.002222psiAngleoftwist(φ)=GtaTL3=0.0154074radWhere,T:Torsionalmoment(300lbf-in)L:Lengthofthecantileverbeam(1500in)a:Sectiondimension(150in)t:Thicknessofthebox(3in)G:Shearmodulusofelasticity(E/2(1+ν)=7.5/2(1+0.3)=2.8846)FEManalysisShearstress(τxy)=0.0022222psi(allelements)Angleoftwist(φ)=(nodaldisplacement)/(distancefromthecentertothenode)=(22155556.1155556.1+)/(2ㆍ2/150)=0.0154074rad※Angleoftwistiscalculatedusingthedisplacementatthenode1.Units:psi,radResultTheoreticalMIDAS/GenShearstress(τxy)0.00222220.0022222Angleoftwist(φ)0.01540740.0154074Example605ReferencesTimoshenko,S.andGoodier,J.N.,“TheoryofElasticity”,McGraw-Hill,NewYork,951,p.299.