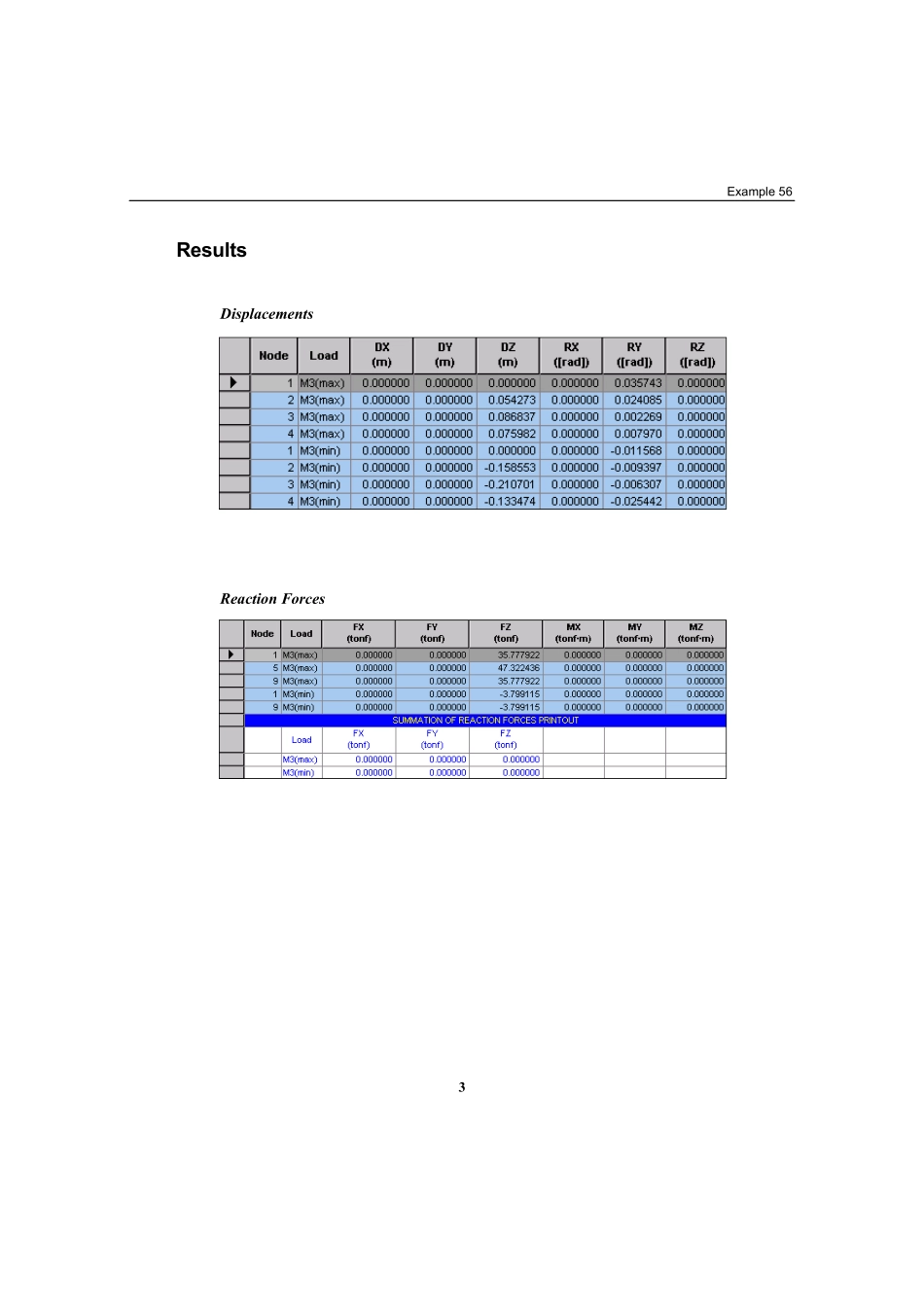
1Example56TitleContinuous2-spanbridgesubjectedtoamovingload(MovingLaodModuleavailableuponrequest)DescriptionAnalyzeacontinuous2-spanbridgesubjectedtoamovingload.StructuralgeometryandanalysismodelVerificationExample2ModelAnalysisType2-DmovingloadanalysisUnitSystemm,tonfDimensionSpanlength20mElementBeamelementMaterialConcreteModulusofelasticityE=2.1×106tonf/m2Poisson’sratioν=0.167SectionPropertySB500×1000mmBoundaryConditionNode1;ConstrainDx,Dz,Dz,RxandRz(pinsupports)Nodes5and9;ConstrainDy,Dz,RxandRz.(Rollersupports)LoadCaseMovingloadsDB-24andDL-24specifiedintheMOCTstandardspecificationforbridgesareapplied.M1;DB-24isapplied.M2;DL-24isapplied.M3;DB-24andDL-24areapplied.Example563ResultsDisplacementsReactionForcesVerificationExample4MemberForcesExample565Momentinfluencelinediagramofthemember(3quartersfromI-end)Momentinfluencelinediagramofthemember(J-end)VerificationExample6Maximumpositive&negativemomentenvelopsofthestructureExample567ComparisonofResultsMaximumpositiveandnegativemomentsofthestructure•Maximumpositivemoment:Occursat3quartersfromI-endoftheelementduetoDB-24loadMy=∑(Concentratedload×Valueofthemomentinfluencelineattheloadpoint)My=4.8×2.08897468+19.2×4.14836+19.2×2.266..712=133.18293tonf-m•Maximumnegativemoment:OccursatJ-endoftheelementduetoDL-24loadMy=Area(negativemoment)×Uniformload+Maximumvalueofthemomentinfluenceline(negativemoment)×Concentratedload(Momentcalculation)+2ndmaximumvalueofthemomentinfluenceline(negativemoment)×Concentratedload(Formomentcalculation)My=(-49.728×1.27)+(-1.92177×10.8)+(-1.921664×10.8)=-104.73452tonf-mUnit:m,tonfResultSAP2000MIDAS/GenPositive(Node3)0.08680.0868Maximumverticaldisplacement(intheZdirection)Negative(Node3)-0.2107-0.2107Positive(EL.23/4pt.)133.18133.18MaximummomentNegative(EL.4jpt.)-104.73-104.73Positive(EL.4jpt.)39.0339.03MaximumshearforceNegative(EL.5Ipt.)-39.03-39.03Positive(Node5)47.32247.322MaximumreactionforceNegative(Node1)-3.799-3.799VerificationExample8Reference“StandardSpecificationforBridges”,MOCT(KoreanMinistryofConstructionandTransportation),1996