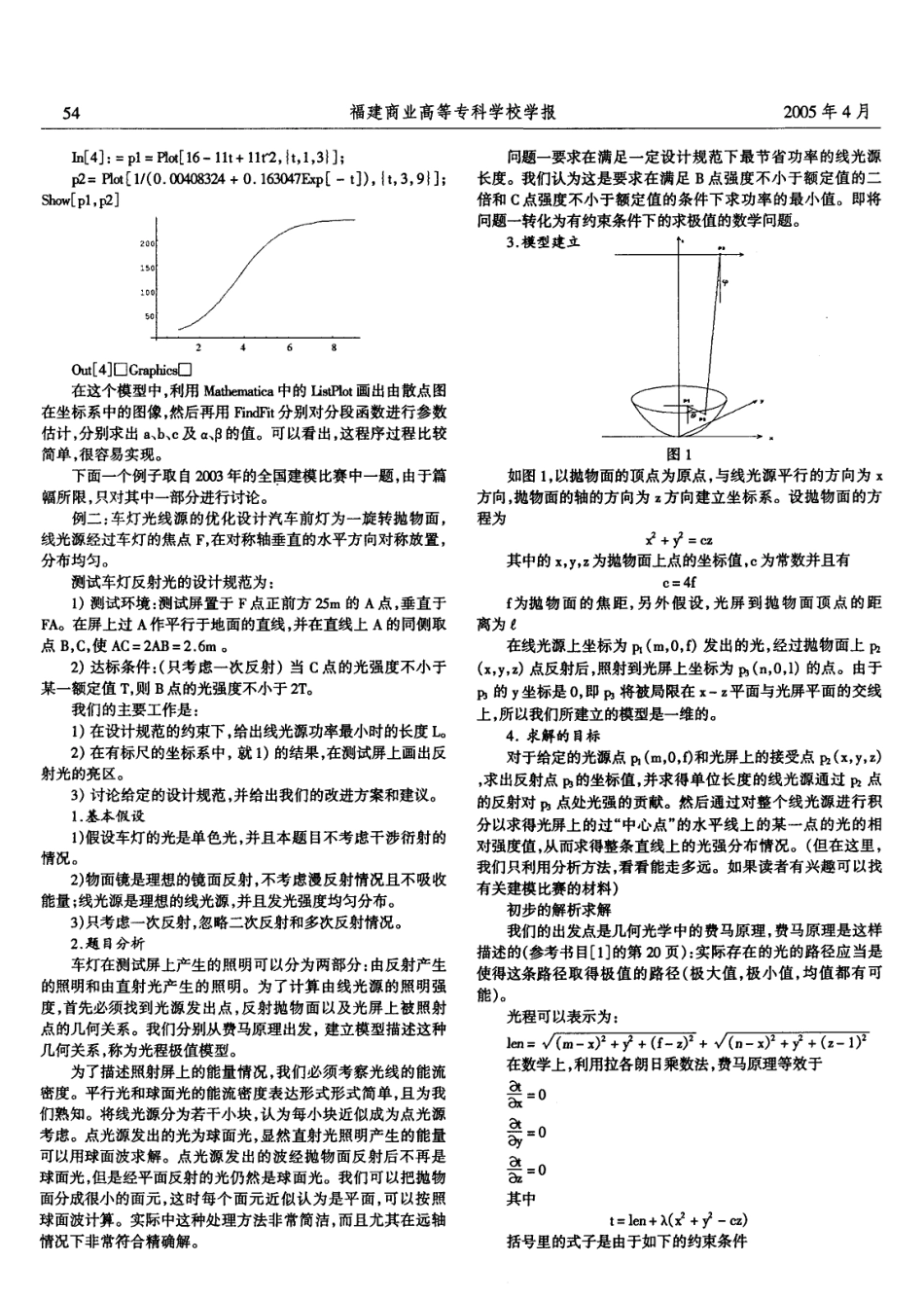
2005年4月第2期陈玲菊‘范建生2:Mathematics在数学建模中的应用Mathematica在数学建模中的应用TheApplicationonMathematicainMathematicalModeling陈玲菊’(1.阂江学院数学系,福建福州350108;2.范建生2*福建商业高等专科学校,福建福州350012)内容提要本文是续《数学软件Mathematics及其概率统计应用)(闽江学院学报,第24卷第五期)之后,从数学建模的角度出发,结合实例介绍了Mathematics在数学建模求解过程中的应用,从而进一步阐明数学软件Mathematics的多方面的运用关键词Mathematica;数学建模;费马原理中图分类号:0245文献标识码:A文章编号:1008一4940(2005)02-0053一03一、简介Mathematics是一种集数学计算、处理与分析为一身的软件,它具有的强大的数值计算、符号计算、数学图形的绘制甚至动画制作的功能,使之在科学研究单位和教学单位中有广泛的用途。近年来,数学建模的蓬勃发展,由于建模过程往往要依靠计算机在计算方面的强大功能,更有效地实现大量的数据、图像处理,而利用Mathematics编写的程序实现这些过程本身并不复杂,而且程序执行的效率比较高,本文将就这一方面结合实例,谈谈Mathematics在数学建模中的应用。二、数学建模的含义什么是数学模型?这方面的定义很多,概括地说,就是用数学语言和方法对实际问题的抽象和描述。牛顿的万有引力定律便是数学模型的一个很好的例子。学习建模就是要学会怎样用自己学到的数学和计算机去解决实际问题。一般来说,一个完整的数学建模过程主要由三部分组成:(1)用适当的数学方法对实际问题进行描述。(2)采用各种数学和计算机手段建立并求解模型。(3)从实际的角度分析模型的结果,考察是否具有实际意义。三、几个应用Mathematics求解数学模型的例子例一:固态酒精发酵动力模型下面利用Mathematics的数据分析函数对固态酒精发酵过程所形成产物的规律进行研究,为简单起见只举确定酒精浓度与发酵时间的关系这一部分。以温度为不变参数(取30),接种量10%,糖化酶用量2801U/克为原料,实验纪录如下表1t的关系为a+bt+ct2(1)。+时...之IL--X利用Mathematics编程计算得到未知数。,b,c,a,日的估计值,从而16一11t+11产10.00408342+0.163047e(2)r尹1.Ll一X方程(2)的图形见codel中的Out[4],根据所建立的方程(2),我们可确定何时酒精浓度取最大,为实现发酵过程的自动控制提供理论支持。codel:城l]:二values二1251,16,134E,17,13811.istplot[values]II,{1,168,1402,389,14113,821,14,112},15,14012...