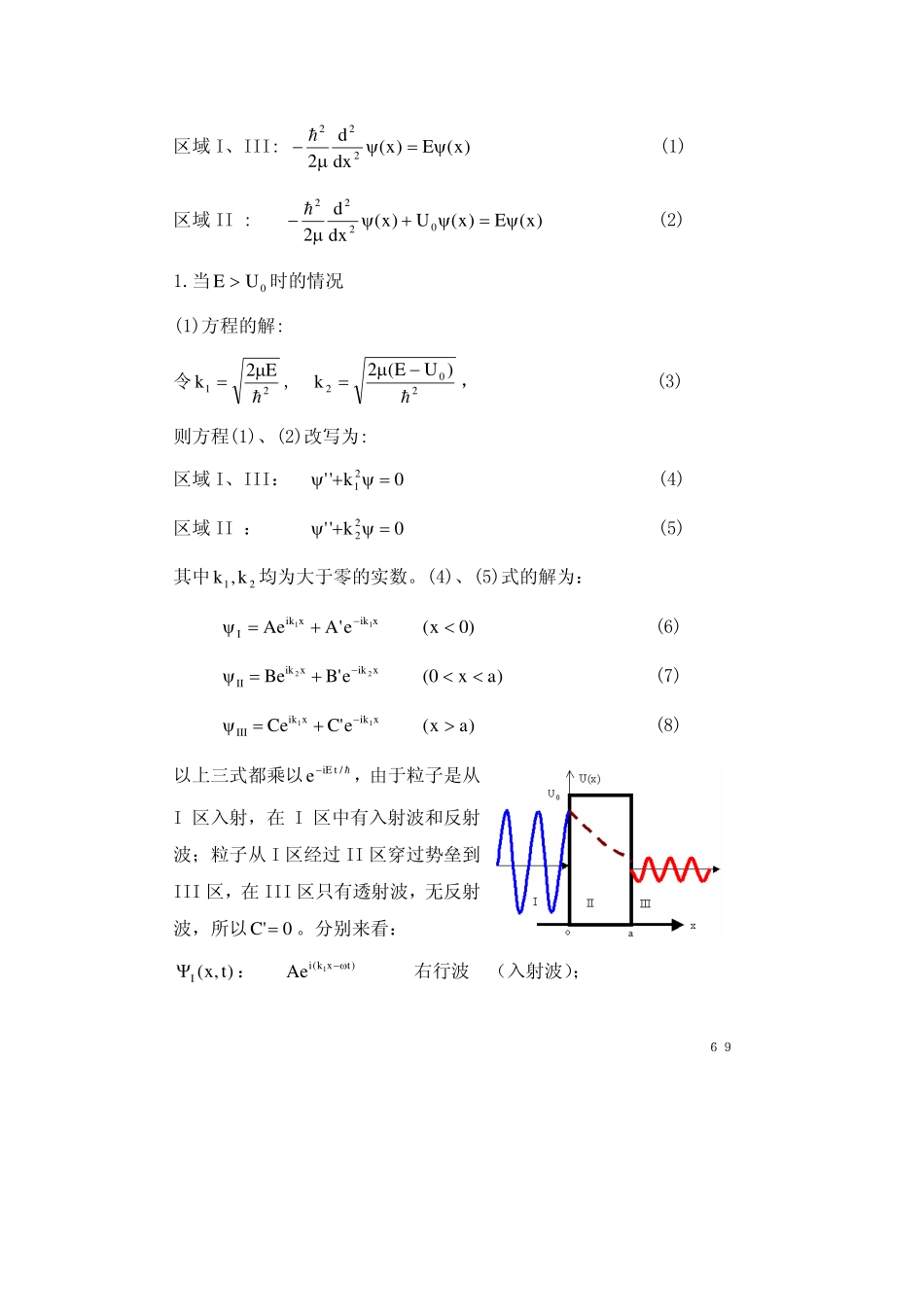
68§2.8势垒贯穿重点:隧穿问题的求解难点:透射和反射系数的计算本节讨论体系的势能在无限远处为有限(下面取为零)、波函数在无限远处不为零的情况,此时体系的能量可取任意值,即组成连续谱。这类问题属于散射问题。已知势场和粒子能量,求波函数。一、一维散射现象⎩⎨⎧><<<=ax,0x0ax0U)x(U0)0U(0>这样的势场称为方形势垒。经典情况:⎩⎨⎧<>粒子全部被势垒反射粒子全部越过势垒UEUE00量子情况:⎩⎨⎧<>也可能贯穿势垒粒子可能被反射回来,可能被反射回来粒子可能越过势垒,也UEUE00称0UE<时粒子通过势垒的现象为隧道贯穿。二、方程的求解粒子的波函数ψ所满足的定态dingeroSchr&&方程为:69区域I、III:)x(E)x(dxd2222ψ=ψμ−h(1)区域II:)x(E)x(U)x(dxd20222ψ=ψ+ψμ−h(2)1.当0UE>时的情况(1)方程的解:令21E2khμ=,202)UE(2kh−μ=,(3)则方程(1)、(2)改写为:区域I、III:0k''21=ψ+ψ(4)区域II:0k''22=ψ+ψ(5)其中21k,k均为大于零的实数。(4)、(5)式的解为:xikxikI11e'AAe−+=ψ)0x(<(6)xikxikII22e'BBe−+=ψ)ax0(<<(7)xikxikIII11e'CCe−+=ψ)ax(>(8)以上三式都乘以h/tiEe−,由于粒子是从I区入射,在I区中有入射波和反射波;粒子从I区经过II区穿过势垒到III区,在III区只有透射波,无反射波,所以0'C=。分别来看:)t,x(IΨ:)txk(i1Aeω−右行波(入射波);70)txk(i1e'Aω+−左行波(反射波),)t,x(IIΨ:)txk(i2Beω−右行波;)txk(i2e'Bω+−左行波,)t,x(IIIΨ:)txk(i1Ceω−右行波(透射波)。(2)几率流密度和粒子数守恒由几率流密度矢量的定义)(2iJ**Ψ∇Ψ−Ψ∇Ψμ≡hv可以得到入射波)txk(i1Aeω−、反射波)txk(i1e'Aω+−和透射波)txk(i1Ceω−的几率流密度矢量的大小分别为:21AkJμ=λh;21DCkJμ=h;21R'AkJμ−=h(9)由几率分布的连续性方程∫∫−=τ∂∂VSxdSJdtw,得0)JJ(JDR=+−λ(入=出)即:222C'AA+=(10)也就是说若有N个粒子在单位时间内通过单位面积流入V,则同时有N个粒子流出V。(3)透射系数和反射系数的定义定义:透射系数22DACJJD=≡λ,反射系数22RA'AJJR=≡λ则:1J/)JJ(DRDR=+=+λ(11)(4)透射系数和反射系数的计算71根据波函数的标准条件,即波函数的有限性,有:)0()0(IIIψ=ψ⇒'BB'AA+=+)0(')0('IIIψ=ψ⇒)'BB(k)'AA(k21−=−)a()a(IIIIIψ=ψ⇒aikaikaik122Cee'BBe=+−)a(')a('IIIIIψ=ψ⇒aik1aikaik2122eCk)e'BBe(k=−−由以上四式可把'A,C表示成A的形式,即:Ae)kk(e)kk(ekk4Caik21...