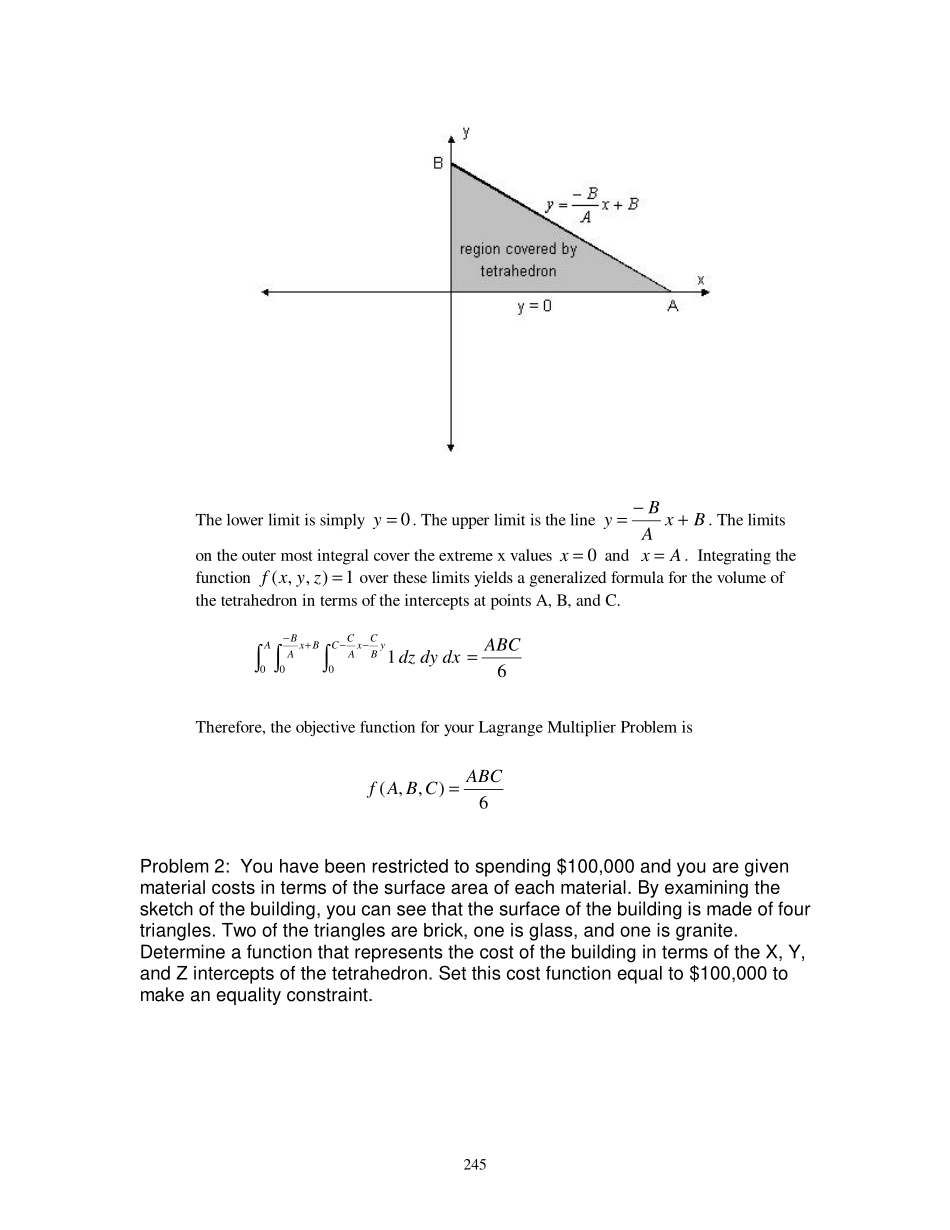
243ModelinginCalculusIIJamesV.MathesonScenario1:OptimizingFiscalResourcesYouhavebeenassignedtoadistrictengineerposition.ThefirstprojectyourunitreceivesistobuildavisitorscenteratarecentlycompletedCorpsofEngineersdamsite.Yourcommanderhasexaminedthebudgetforcompletingthevisitorscenteranddecidedthatyoucanuseroughly$100,000worthofmaterialtocompletetheoutershellofthebuilding.Thearchitect’sconceptforthedesignofthebuildingisthatitwillbearighttetrahedron.Thefloorofthetetrahedronistobeconstructedoutofgraniteblocks,twoofthewallsaretobemadeofbrickandoneofthewallsistobemadeofglass.Yourcommanderhasaskedyoutouseyourknowledgeofmultipleintegralsandoptimizationtocomeupwitharoughestimateofthemaximumvolumeofabuildingthatcanbeconstructedintheshapeofatetrahedronfor$100,000.Heprovidesyouwiththefollowingsketchandachartthathasthecostofthematerialsyouwillusetoconstructthebuilding.244MaterialCost:$persquaremeterofsurfaceareaBrick3Granite8Glass2Thisisyourfirstmajorprojectasadistrictengineerandyouaredeterminedtocreatethebestvisitorscentereverbuiltbyadamsite.Inordertomakeagoodestimateofthemaximumvolumeforthebuilding,youdecidetousethemethodofLagrangetooptimizethevolumeofthebuildingsubjecttotheequalityconstraintof$100,000worthofbuildingmaterials.Problem1:Agoodplacetobeginanyoptimizationproblemiswithanobjectivefunction.Inthiscase,thegoaloftheprojectistooptimizethevolumeofthebuilding.Fromthesketchyoureceived,theshapeofthebuildingisarighttetrahedron.Useamultipleintegraltofindageneralizedfunctionrepresentingthevolumeofarighttetrahedron.Solution1:Atripleintegralcanbeusedtofindthevolumeofthetetrahedron.Thelimitsoftheinnermostintegralcomefromthex-yplaneatthebottomofthebuildingandthePlanecontainingthepointsA,B,andCwhichcreatestheroofofthebuilding.TofindtheequationoftheplanecontainingA,B,andC,itisnecessarytocreatevectorsABandAC.Thevectorsarethencrossedtofindavectornormaltotheplane.Fromthere,thepointnormalequationoftheplaneisusedtofindtheupperlimitfortheinnermostintegral.Thustheinnerintegrallimitsare0=z...