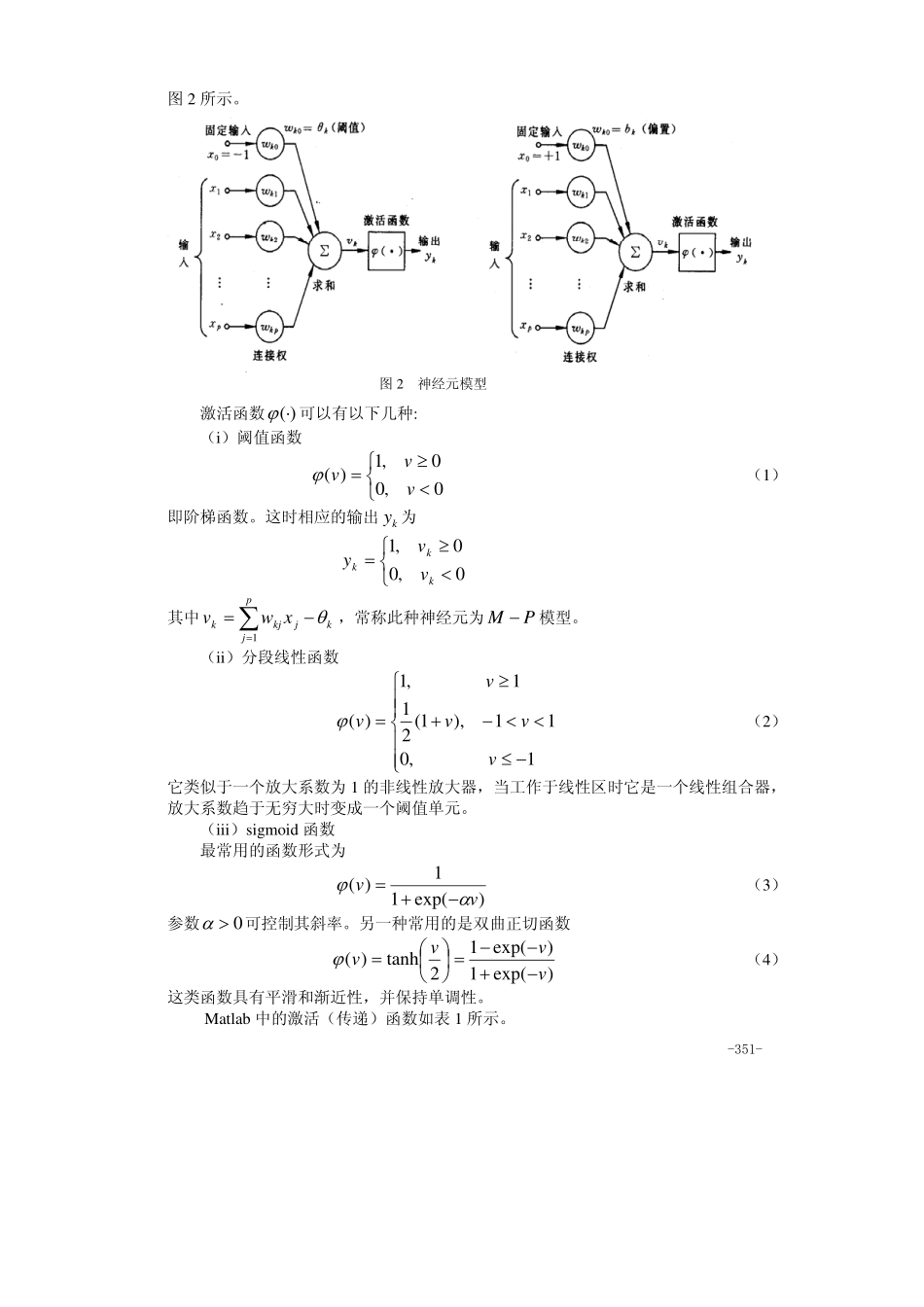
-350-第十九章神经网络模型§1神经网络简介人工神经网络是在现代神经科学的基础上提出和发展起来的,旨在反映人脑结构及功能的一种抽象数学模型。自1943年美国心理学家W.McCulloch和数学家W.Pitts提出形式神经元的抽象数学模型—MP模型以来,人工神经网络理论技术经过了50多年曲折的发展。特别是20世纪80年代,人工神经网络的研究取得了重大进展,有关的理论和方法已经发展成一门界于物理学、数学、计算机科学和神经生物学之间的交叉学科。它在模式识别,图像处理,智能控制,组合优化,金融预测与管理,通信,机器人以及专家系统等领域得到广泛的应用,提出了40多种神经网络模型,其中比较著名的有感知机,Hopfield网络,Boltzman机,自适应共振理论及反向传播网络(BP)等。在这里我们仅讨论最基本的网络模型及其学习算法。1.1人工神经元模型图1表示出了作为人工神经网络(artificialneuralnetwork,以下简称NN)的基本单元的神经元模型,它有三个基本要素:图1神经元模型(i)一组连接(对应于生物神经元的突触),连接强度由各连接上的权值表示,权值为正表示激活,为负表示抑制。(ii)一个求和单元,用于求取各输入信号的加权和(线性组合)。(iii)一个非线性激活函数,起非线性映射作用并将神经元输出幅度限制在一定范围内(一般限制在)1,0(或)1,1(−之间)。此外还有一个阈值kθ(或偏置kkbθ−=)。以上作用可分别以数学式表达出来:∑==pjjkjkxwu1,kkkuvθ−=,)(kkvyϕ=式中pxxx,,,21L为输入信号,kpkkwww,,,21L为神经元k之权值,ku为线性组合结果,kθ为阈值,)(⋅ϕ为激活函数,ky为神经元k的输出。若把输入的维数增加一维,则可把阈值kθ包括进去。例如∑==pjjkjkxwv0,)(kkuyϕ=此处增加了一个新的连接,其输入为10−=x(或1+),权值为kkwθ=0(或kb),如-351-图2所示。图2神经元模型激活函数)(⋅ϕ可以有以下几种:(i)阈值函数⎩⎨⎧<≥=0,00,1)(vvvϕ(1)即阶梯函数。这时相应的输出ky为⎩⎨⎧<≥=0,00,1kkkvvy其中∑=−=pjkjkjkxwv1θ,常称此种神经元为PM−模型。(ii)分段线性函数⎪⎪⎩⎪⎪⎨⎧−≤<<−+≥=1,011),1(211,1)(vvvvvϕ(2)它类似于一个放大系数为1的非线性放大器,当工作于线性区时它是一个线性组合器,放大系数趋于无穷大时变成一个阈值单元。(iii)sigmoid函数最常用的函数形式为)exp(11)(vvαϕ−+=(3)参数0>α可控制其斜率。另一种常用的是双曲正切函数)exp(1)exp(12tanh)(vvvv−+−−=⎟⎠⎞⎜...