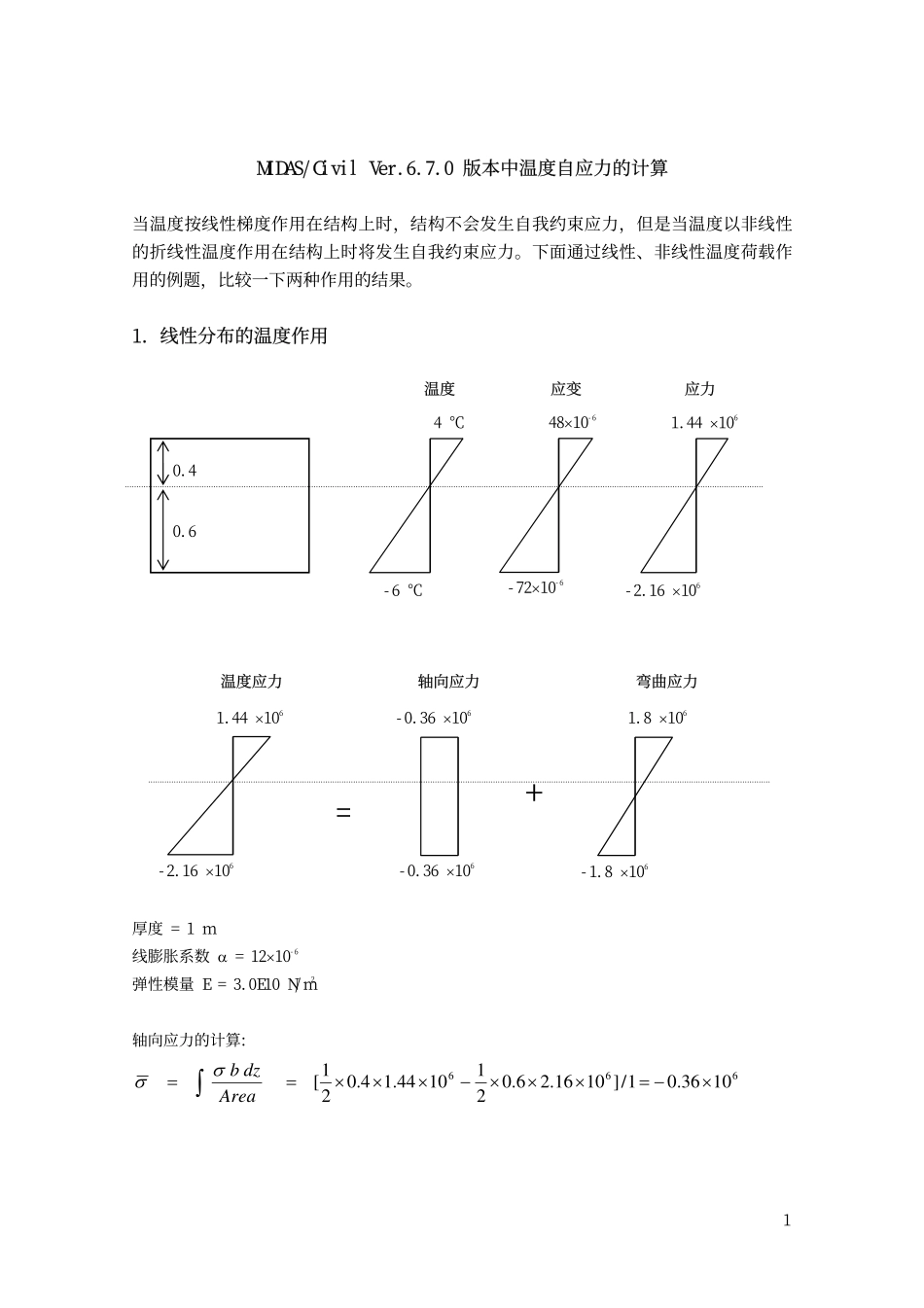
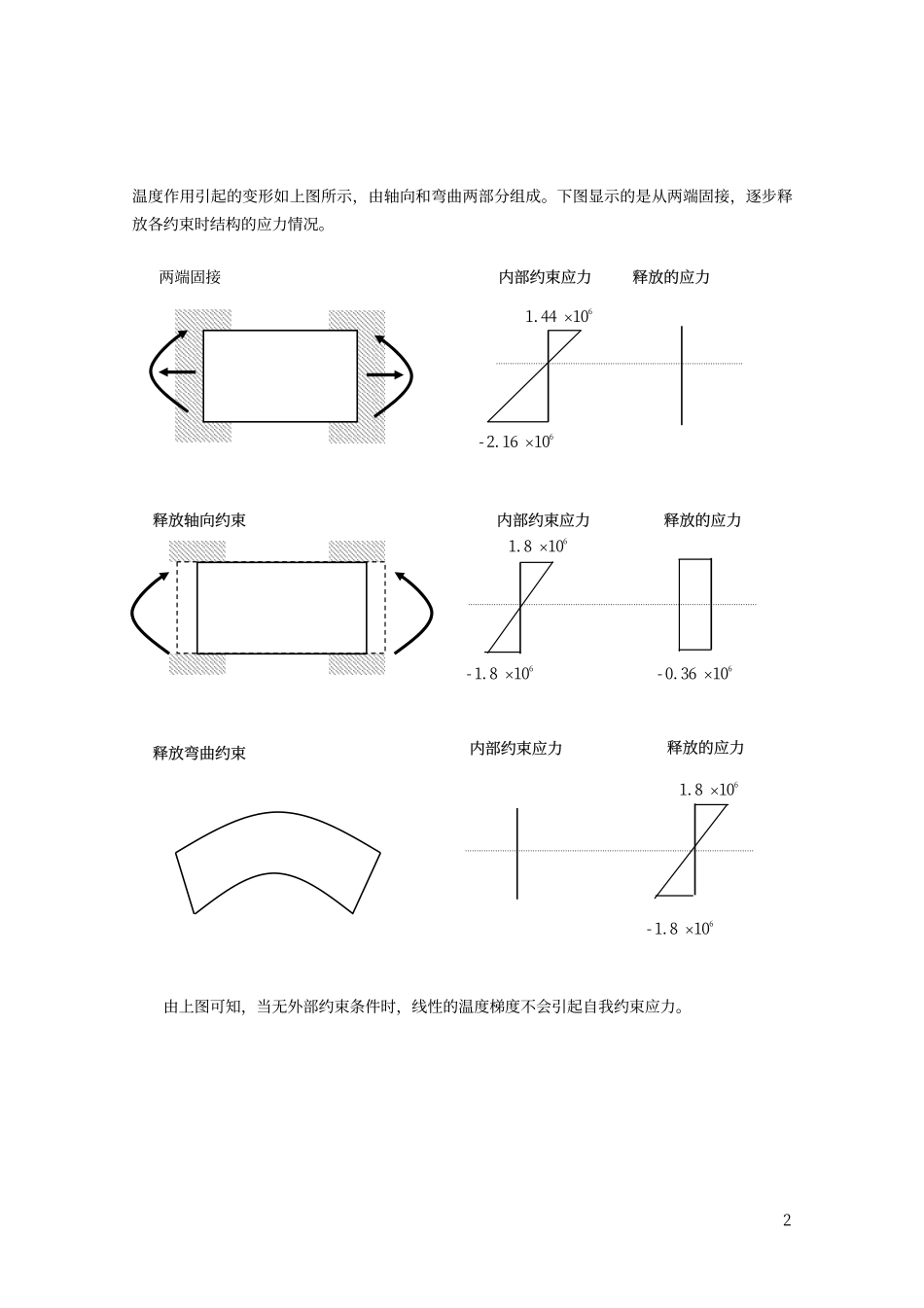
MIDAS/CivilVer.6.7.0版本中温度自应力的计算当温度按线性梯度作用在结构上时,结构不会发生自我约束应力,但是当温度以非线性的折线性温度作用在结构上时将发生自我约束应力。下面通过线性、非线性温度荷载作用的例题,比较一下两种作用的结果。1.线性分布的温度作用温度应变应力48×10-61.44×1064℃0.60.4-72×10-6-2.16×106-6℃温度应力1.44×106=1.8×106弯曲应力-0.36×106+轴向应力-0.36×106-2.16×106-1.8×106厚度=1m线膨胀系数α=12×10-6弹性模量E=3.0E10N/m2轴向应力的计算:6661036.01/]1016.26.0211044.14.021[×−=×××−×××==∫Areadzbσσ1温度作用引起的变形如上图所示,由轴向和弯曲两部分组成。下图显示的是从两端固接,逐步释放各约束时结构的应力情况。释放的应力两端固接内部约束应力1.44×106-2.16×106释放轴向约束释放的应力内部约束应力-1.8×1061.8×106-0.36×106释放的应力内部约束应力释放弯曲约束1.8×106-1.8×106由上图可知,当无外部约束条件时,线性的温度梯度不会引起自我约束应力。22.非线性分布的温度作用下图为截面上作用非线性温度时的应力分布情况。温度应变应力48×10-61.44×1064℃0.60.472×10-62.16×1066℃温度应力弯曲应力轴向应力1.44×1060.936×1060.504×106=+-0.936×1062.16×1061.224×1060.936×106将温度应力也用轴向应力和弯曲应力表达。轴向应力的计算:66610936.01/]1016.26.0211044.14.021[×=×××+×××==∫Areadzbσσ由弯曲应力图计算等效弯矩:∫××××−×××××==)4.0(52.010936.021)14.031(14.010504.02166dzzbMTσ66100888.0)34.03266.0(34.010224.121×=×+××××+3相当于等效弯矩引起的弯曲应力:626105328.06/1100888.0×=×==zMTσ同样,下图显示的是从两端固接,逐步释放各约束时结构的应力情况。释放的应力内部约束应力两端固接1.44×1062.16×106内部约束应力释放的应力释放轴向约束0.936×106内部约束应力释放的应力释放弯曲约束0.5328×1060.504×106-9.36×1051.224×106-0.5328×1061.0368×106-8.2944×1056.912×1054如上图所示,在最后释放弯曲约束时,由等效弯矩引起的应力将被释放掉,而结构即使没有外部弯矩作用同样会存在残余应力。非常重要的是,对残余的应力积分结果为‘0’,说明即使没有产生构件内力,也会由于纤维间自我约束的作用产生内部的应力。结论:在非线性温度梯度作用下,即使没有对结构的弯曲约束,截面内也将产生应力。温度自应力影响截面内的应力分布,对裂缝比较敏感的结构以及联合截面结构的影响将是不可忽视的。MIDAS/Civilv6.7.1的分析结果Bend(+z)(0.5)Bend(-z)(-0.5)(+0.1)中心位置(-0.1)1.04E+066.91E+05-8.29E+05-5.76E+05-3.230e+0055