电路分析基础(13).pdfVIP免费

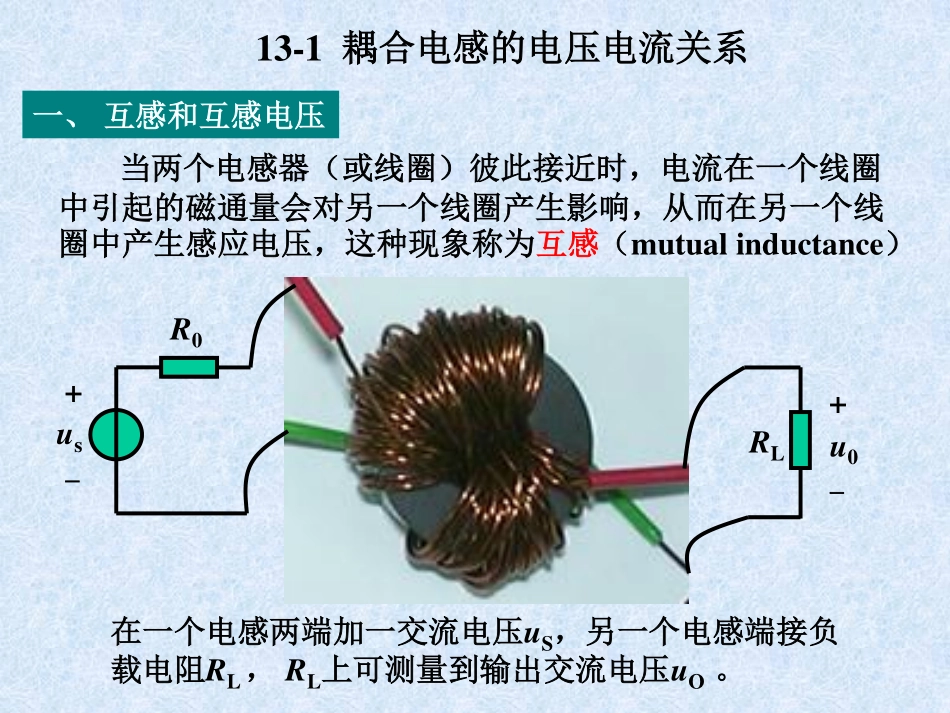
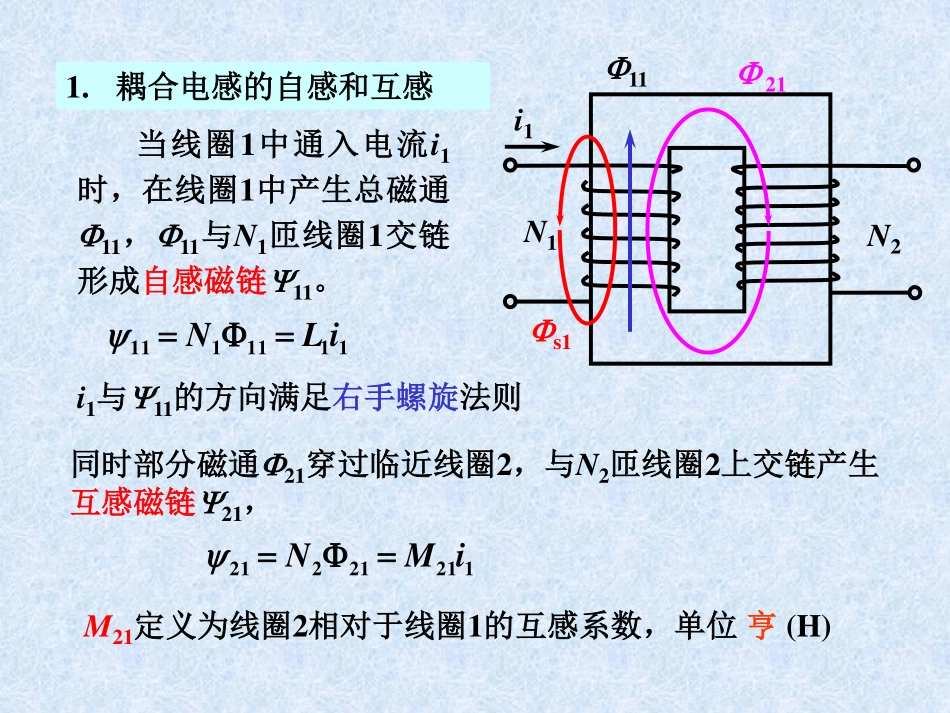
第13章含耦合电感的电路分析重点：耦合电感的电压电流关系耦合电感的串并联耦合电感的去耦等效电路13-1耦合电感的电压电流关系一、互感和互感电压当两个电感器（或线圈）彼此接近时，电流在一个线圈中引起的磁通量会对另一个线圈产生影响，从而在另一个线圈中产生感应电压，这种现象称为互感（mutualinductance）在一个电感两端加一交流电压uS，另一个电感端接负载电阻RL，RL上可测量到输出交流电压uO。+-usR0RL+-u0当线圈1中通入电流i1时，在线圈1中产生总磁通F11，F11与N1匝线圈1交链形成自感磁链11。1.耦合电感的自感和互感i1与11的方向满足右手螺旋法则1111111iLNF同时部分磁通F21穿过临近线圈2，与N2匝线圈2上交链产生互感磁链21，12121221iMNFM21定义为线圈2相对于线圈1的互感系数，单位亨(H)N1N2F11F21Fs1i1N1N2F22F12Fs2i2当线圈2也通入电流i2时，也会产生自感磁链22，在线圈1上产生互感磁链122222222iLNF21212112iMNF两个线圈同时存在i1和i2，通过每个线圈的总磁链等于自感磁链叠加互感磁链，是电流i1和i2单独作用时磁链的叠加。i12121112111iMiL2212122212iLiMN1N2i2i1±±2、互感的性质①从电磁场理论可以证明，对于线性电感M12=M21=M②互感系数M只与两个线圈的几何尺寸、匝数、相互位置和周围的介质磁导率有关，如其他条件不变时，有MN1N2（LN2）3、耦合系数(couplingcoefficient)kk表示两个线圈磁耦合的紧密程度。全耦合:k=121defLLMk即11=21，22=12可以证明，k1。无耦合:k=0紧耦合:k接近于1松耦合:k很小时4、耦合电感的自感电压与互感电压根据电磁感应定律，当电流i1和i2随时间变化时，电感中磁链也随时间变化，将在电感中产生感应电动势。dtdu21112111MiiL22122212iLMi21112111dtdiMdtdiLuuu22122212dtdiLdtdiMuuuN1N2i2i1+–u1+–u221112111dtdiMdtdiLuuu22122212dtdiLdtdiMuuuN1N2i2i1+–u1+–u2dd1111tiLudd2222tiLudd121tiMudd212tiMu自感电压互感电压互感电压的正负号取决于磁通量方向，当i1和i2在耦合线圈中产生的磁场方向相同而相互增强时，互感电压的符号为正。反之为负。N1N2i2i1N1N2i2i1dd121tiMudd212tiMu上图dd121tiMudd212tiMu下图二、互感线圈的同名端具有互感的线圈两端的电压包含自感电压和互感电压，表达式的符...