电路分析基础(9).pdfVIP免费

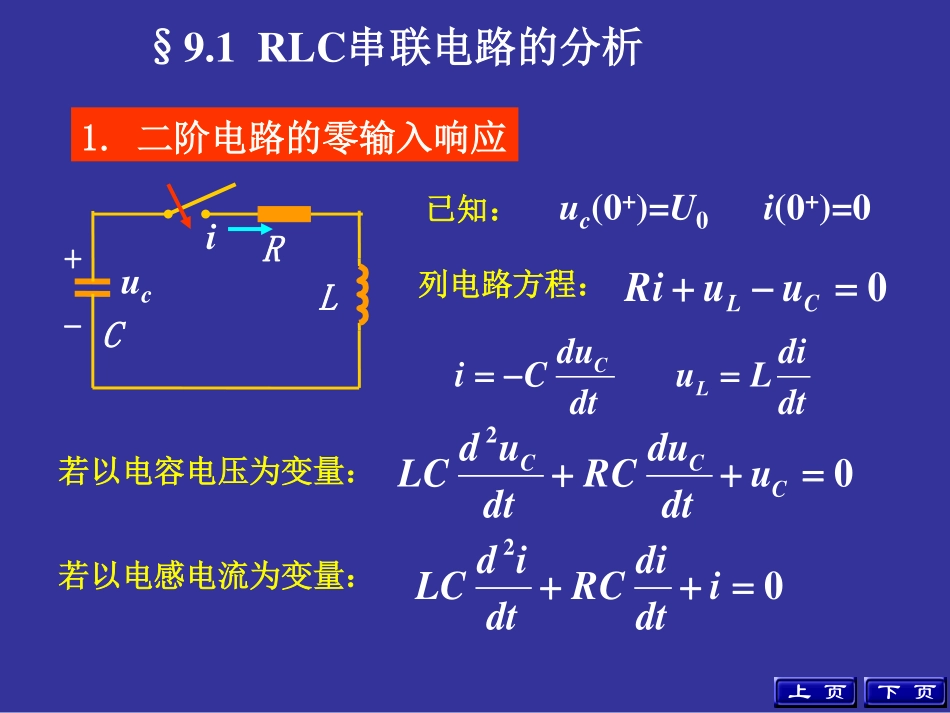
第9章二阶电路分析2.用经典方法对微分方程求解。重点：1.二阶电路微分方程的建立；uc(0+)=U0i(0+)=002CCCudtduRCdtudLC已知：1.二阶电路的零输入响应RLC+-iuc若以电容电压为变量：列电路方程：0CLuuRidtdiLudtduCiLC若以电感电流为变量：02idtdiRCdtidLC下页上页§9.1RLC串联电路的分析012RCPLCP特征方程：电路方程：02CCCudtduRCdtudLC以电容电压为变量时的初始条件：uc(0+)=U0i(0+)=000tCdtdu以电感电流为变量时的初始条件：i(0+)=0uc(0+)=U0)0()0(00UdtdiLuutLCLUdtdit00下页上页2.零状态响应的三种情况二个不等负实根2CLR二个相等负实根2CLR二个共轭复根2CLRLCLRRP2/42过阻尼临界阻尼欠阻尼LCLRLR1)2(22特征根：下页上页2)1(CLRtptpceAeAu21210210)0(UAAUuc02211)0(APAPdtduC0121201221UPPPAUPPPA)(2112120ttCPePPePPPUu下页上页)(2112120ttcPPePePPPUuU0tuctPePPUP11202tPePPUP21201设|P2|>|P1|下页上页)()(21120ttccppeePPLUdtduCit=0+ic=0,t=ic=0ic>0t=tm时ic最大tU0uctm2tmuLic00t>tmi减小,uL<0t=2tm时uL最大)()(2121120ttLppePePPPUdtdiLu)(2112120ttcPPePePPPUu0,,00LLutUut下页上页iC=i为极值时的tm即uL=0时的t,计算如下:0)(2121ttppePeP2112pppptmln由duL/dt可确定uL为极小时的t.0)(212221tptpePePmtt2)()(2121120ttLppePePPPUdtdiLu21122pppptlnmmtPtPeePP2112下页上页能量转换关系RLC+-RLC+-tU0uctm2tmuLic0tmuc减小，i减小.下页上页2)2(CLR特征根为一对共轭复根LCLRLRP1)2(22jP)(1)(20谐振角频率衰减系数令：LCLR)(220固有振荡角频率则uc的解答形式：)(tjtjttptpceAeAeeAeAu212121经常写为：)sin(tAeutcA，为待定常数下页上页0cossin)(0)0(sin)0(00AAdtduUAUucc由初始条件arctgUA，sin0ω，ω０，δ间的关系:0sin00UAδωω000sin()tcuUet下页上页)sin(00teUutc为包络线的正弦函数。是其振幅以tceUu00t=0时uc=U0uc零点：t=-，2-...n-t-2-...