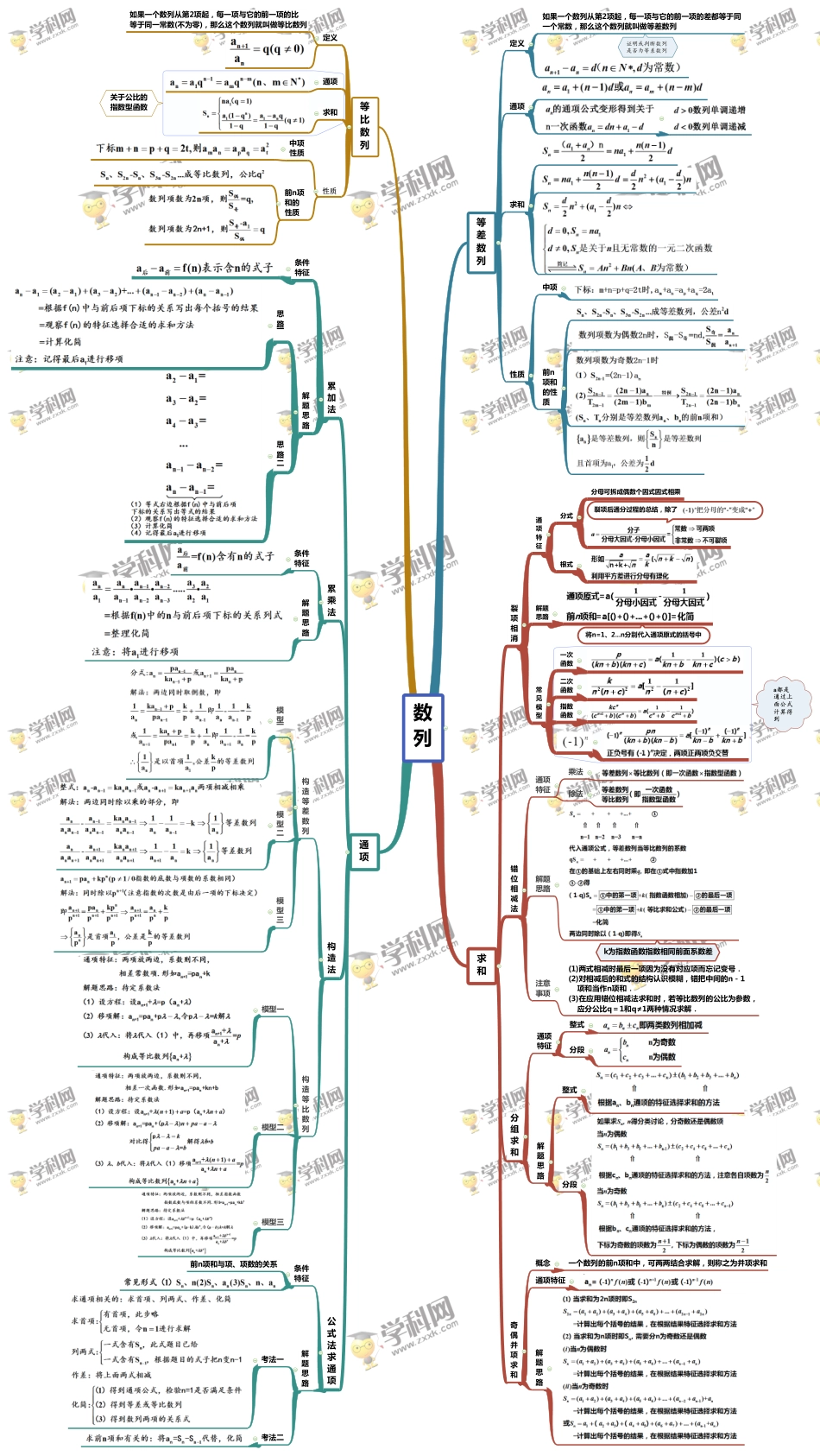
证明或判断数列是否为等差数列关于公比的指数型函数裂项后通分过程的总结,除了将n=1、2...n分别代入通项原式的括号中a都是通过上面公式计算得到k为指数函数指数相同前面系数差数列通项等差数列定义通项求和性质中项前n项和的性质如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列等比数列定义通项求和性质如果一个数列从第2项起,每一项与它的前一项的比等于同一常数(不为零),那么这个数列就叫做等比数列中项性质前n项和的性质求和累加法条件特征解题思路思路一思路二累乘法条件特征解题思路构造法构造等差数列构造等比数列模型一模型二模型三模型一模型二模型三裂项相消通项特征解题思路常见模型分式根式分母可拆成偶数个因式因式相乘一次函数二次函数指数函数错位相减法通项特征解题思路注意事项乘法除法(1)两式相减时最后一项因为没有对应项而忘记变号.(2)对相减后的和式的结构认识模糊,错把中间的n-1项和当作n项和.(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比q=1和q≠1两种情况求解.分组求和通项特征解题思路整式分段整式分段公式法求通项条件特征解题思路前n项和与项、项数的关系考法一考法二奇偶并项求和通项特征解题思路概念一个数列的前n项和中,可两两结合求解,则称之为并项求和